Addition von Brüchen mit verschiedenen Nennern

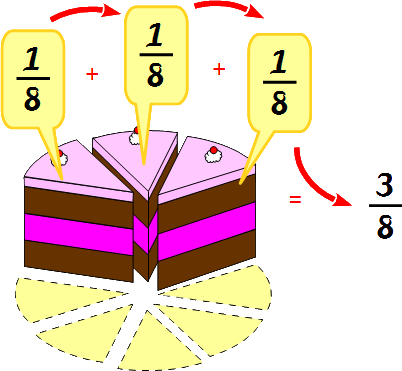
Deine Oma hat eine Torte gebacken und in 8 Stücke geteilt. Ein Tortenstück entspricht 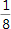der gesamten Torte. Du bist hungrig und isst zuerst ein Tortenstück und anschließend noch mal ein Tortenstück. Du hast nun 2-mal 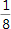-Stück der Torte gegessen. Mit Sicherheit wirst du sagen, dass du 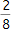gegessen hast. Kurze Zeit später isst du noch einmal ein Stück. Nun hast du 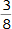gegessen. Du hast dabei schon die Addition von Brüchen angewandt, ohne groß zu wissen, wie sie überhaupt funktioniert. Im Folgenden werden wir uns nun die Vorgehensweise der Addition genauer ansehen.

Das Wort Addition stammt von dem lateinischen Wort »addere« und bedeutet »hinzufügen«. Oft wird sie auch als »Plus-Rechnen« bezeichnet, da das Rechenzeichen für die Addition das Pluszeichen + ist. Die einzelnen Brüche werden bei einer Addition Summanden genannt. Sie werden entsprechend der Anzahl durchnummeriert. Der erste Bruch ist der erste Summand, der zweite Bruch ist der zweite Summand und so weiter. Wenn du alle Summanden addierst oder zusammenzählst, erhältst du die Summe. So wird das Ergebnis der Addition genannt.

1. Summand + 2. Summand = Summe

1. Bruch + 2. Bruch = Ergebnis

Bei der Addition von Brüchen wird zu einem Bruch ein oder mehrere Brüche hinzugezählt (addiert). Du kannst jedoch nicht beliebige Brüche miteinander addieren, so wie du es von der Addition mit Zahlen gewohnt bist: Die Brüche müssen beim Addieren den gleichen Nenner (Hauptnenner) haben. Man nennt dies gleichnamige Brüche. Sind die Nenner unterschiedlich (also nicht gleichnamig), so musst du zuerst nach einem gemeinsamen Hauptnenner suchen. Ein Hauptnenner ist das kleinste gemeinsame Vielfache (kgV) aller bei einer Rechnung beteiligten Nenner. Er ist also ein Nenner, in dem alle Nenner deiner Rechnung enthalten sind. Dazu werden beide Brüche entsprechend erweitert bzw. gekürzt, um das kleinste gemeinsame Vielfache, den Hauptnenner, zu bekommen. Dieser Vorgang nennt man gleichnamig machen. Anschließend werden nur die Zähler der einzelnen Brüche addiert, der gleichnamige Hauptnenner wird beibehalten.

Stelle 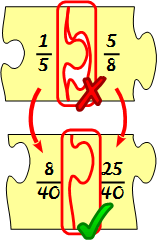dir bei der Addition vor, die einzelnen Brüche wären Puzzleteile. Je nach Nenner sieht die Nase und die Öffnung der Puzzleteile anders aus. Nur Brüche mit gleichem Nenner bzw. Puzzleteile mit gleichen Nasen und Öffnungen passen somit zusammen.

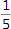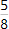Du kannst die beiden Brüche und nicht direkt miteinander addieren, da sie verschiedene Nenner haben. Die Nase ist viel kleiner als die Öffnung, sie passen nicht zusammen. Erweiterst du beide Brüche auf den gemeinsamen Hauptnenner (in diesem Beispiel auf 40), sind die Nenner bzw. die Nase und die Öffnung der Puzzleteile wieder gleich. Jetzt kannst du diese beiden Brüche direkt miteinander addieren. Die Nase und die Öffnung passen wieder zusammen.

So addierst du Brüche mit verschiedenen Nennern:	So sieht's aus:
Diese beiden Brüche sollen miteinander addiert werden.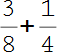
1. Schaue dir zuerst die Nenner der Brüche an. Die Nenner von diesen beiden Brüchen sind verschieden.
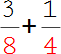2. Um diese Brüche zu addieren, benötigst du einen gemeinsamen Nenner, in dem sowohl die 4 als auch die 8 steckt. Der kleinste gemeinsame Nenner (Hauptnenner) wäre 8, da hier sowohl die 4 als auch die 8 enthalten ist.
3. Schauen wir uns die Brüche genauer an: Da der Hauptnenner 8 ist, kannst du den ersten Bruch lassen, wie er ist. Sein Nenner (8) ist bereits der Hauptnenner.
4. Den zweiten Bruch musst du mit 2 (4 · 2 = 8) erweitern, um auf den Hauptnenner von 8 zu kommen.
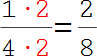5. Jetzt sind die Nenner von beiden Brüchen gleich, du kannst mit der Addition beginnen.
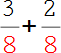6. Addiere zuerst die beiden Zähler: 3 + 2 = 5.
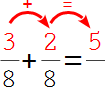7. Der gemeinsame Nenner (8) wird beibehalten.
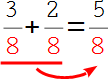8. Dein Ergebnis lautet .

Beim Addieren von Brüchen mit verschiedenen Nennern müssen die Nenner zuerst durch Erweitern bzw. Kürzen gleichnamig gemacht werden. Anschließend werden nur die Zähler der einzelnen Brüche addiert, der gleichnamige Hauptnenner wird beibehalten.