Diagonale (Fläche)
Das Wort Diagonale setzt sich aus den beiden Wörtern »dia« und »gonia« zusammen. Der erste Wortteil »dia« ist altgriechischen und bedeutet »durch«. Der zweite Wortteil »gonia« ist ebenfalls altgriechischen und bedeutet »Ecke, Winkel«. Daher bedeutet Diagonale »durch die Ecke« bzw. »durch den Winkel«. Eine Diagonale ist eine Strecke, die zwei nicht benachbarte Ecken von Flächen miteinander verbindet.
Du kannst die Anzahl der Diagonalen (d) in einem Vieleck berechnen: Du subtrahierst von er Anzahl der Ecken (n) den Wert 3 und multiplizierst das Ergebnis mit der Anzahl der Ecken. Anschließend dividierst du dein Ergebnis durch 2, da du die Diagonalen sonst doppelt zählen würdest. Jede der n Ecken kann mit weiteren n - 3 Ecken durch eine Diagonale verbunden werden. Die betrachtete Ecke kann mit sich selbst und nicht mit den beiden Nachbarecken eine Diagonale haben, daher n – 3.
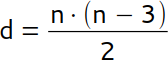
| So berechnest du die Anzahl der Diagonalen: | So sieht's aus: |
|---|---|
| Du sollst die Anzahl der Diagonalen in einem 6-Eck berechnen. Dazu benötigst du folgende Formel: |  |
|
1.
Setze in die Formel anstelle dem n den Wert des n die Anzahl der Ecken ein: n = 6. |
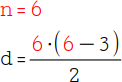 |
|
2.
Berechne zuerst die Klammer im Zähler: 6 – 3 = 3. |
 |
|
3.
Berechne anschließend den Zähler: 6 · 3 = 18. |
 |
|
4.
Berechne anschließend den Bruch: 18 : 2 = 9. |
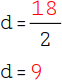 |
|
5.
Das 6-Eck hat also 9 Diagonalen. |
d=9 |
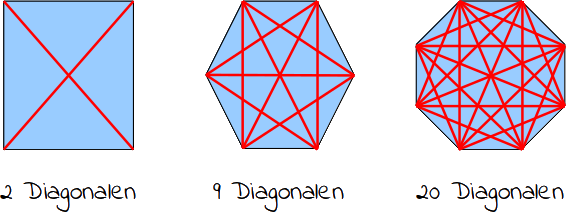
Die Fläche muss mindestens 4 Ecken haben, damit du überhaupt eine Diagonale einzeichnen kannst. Daher hat das Dreieck keine Diagonalen.
Das könnte dich auch interessieren
Du hast einen Fehler gefunden oder möchtest uns eine Rückmeldung zu diesem Eintrag geben? Rückmeldung geben