Satz des Heron

Der Satz des Heron ist ein Satz in der Geometrie. Er ist nach dem antiken Mathematiker Heron von Alexandria benannt (lebte vermutlich im 1. Jahrhundert). Mit dem Satz des Heron kannst du den Flächeninhalt eines Dreiecks nur aus den drei Seitenlängen a, b und c berechnen.

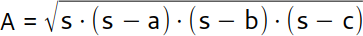
Um den Flächeninhalt berechnen zu können, benötigst du noch den die Hälfte des Umfangs des Dreiecks. Dieser wird in der Formel mit dem s dargestellt. Dazu addierst du die Länge aller drei Seiten zusammen und dividierst am Schluss das Ergebnis noch durch 2:

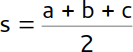
So wendest du den Satz des Heron an:	So sieht's aus:
In einem Dreieck sind alle Seite gegeben. Du sollst nun den Flächeninhalt bestimmt.	a=3cm b=4cm c=5cm
1. Als erstes rechnest du den Faktor s aus: Addiere zuerst alle drei Seitenlängen zusammen: 3cm + 4 cm + 5 cm = 12 cm.
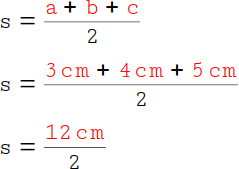2. Dividiere nun den Umfang durch 2: 12 cm : 2 = 6 cm.
3. Setze nun alle Werte in die Formel ein.
4. Berechne die erste Klammer: 6 cm – 3 cm = 3 cm.
5. Berechne die zweite Klammer: 6 cm – 4 cm = 2 cm.
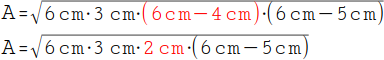6. Berechne die dritte Klammer: 6 cm – 5 cm = 1 cm.
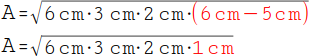7. Berechne nun die Multiplikation unter der Wurzel. Multipliziere zuerst die Zahlen: 6 · 3 · 2 · 1 = 36.
8. Multipliziere anschließend die Einheiten: cm · cm · cm · cm = cm⁴. Du erhältst dabei ein cm hoch 4 (cm⁴), was uns aber nicht weiter stört.
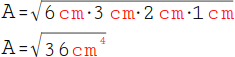9. Ziehe nun die Wurzel: √36cm² = 6 cm². Aus dem cm⁴ ist nun ein cm² geworden.
10. Der Flächeninhalt beträgt 6 cm².	A=6cm²