zyklische Zahl
Eine zyklische Zahl ist eine n-stellige natürliche Zahl mit einer besonderen, witzigen Eigenschaft: Wird diese Zahl mit einer natürlichen Zahl von 1 bis n multipliziert, so besteht das Produkt wieder aus den gleichen Ziffern wie die Ausgangszahl in derselben zyklischen Reihenfolge.
Der US-amerikanische Mathematiker Leonard Eugene Dickson (1874-1954) fand heraus, dass alle zyklischen Zahlen Perioden von periodischen Zahlen sind, die man als Kehrwert bestimmter Primzahlen gewinnen kann. Das bedeutet, dass der Kehrwert einer Primzahl ein periodisches Ergebnis hervorbringt, dass aus sich immer wiederholenden Ziffern (Periode) besteht. Wenn du nun die Ziffernfolge der Periode mit den Zahlen von 1 bis zur Anzahl der Stellen dieser Periode multiplizierst, so besteht das Produkt wieder aus den gleichen Ziffern, die sogar in derselben Reihenfolge stehen.
Die Zahlen, die Perioden einer zyklischen Zahl erzeugen, werden auch Generatorzahlen genannt und sind beispielsweise 7, 17, 19, 23, 29, 47, 59, 61, 97 oder 109.
Die kleinste und bekannteste zyklische Zahl ist die 142857. Sie entsteht, wenn du den Kehrwert der Primzahl 7 bildest: 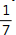 = 0,14285714285714… und das Ergebnis als Periode aufschreibst:
= 0,14285714285714… und das Ergebnis als Periode aufschreibst: 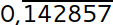 . Genau diese 6 Ziffern der Periode bilden die zyklische, 6-stellige Zahl 142857. Multiplizierst du sie mit 2, 3, 4, 5 und 6, so ist das Ergebnis eine zyklische Wiederholung aus den selben Ziffern: 2 ⋅ 142.857 = 285.714 bzw. 3 ⋅ 142.857 = 428.571. Die jeweiligen Produkte würden den Brüchen
. Genau diese 6 Ziffern der Periode bilden die zyklische, 6-stellige Zahl 142857. Multiplizierst du sie mit 2, 3, 4, 5 und 6, so ist das Ergebnis eine zyklische Wiederholung aus den selben Ziffern: 2 ⋅ 142.857 = 285.714 bzw. 3 ⋅ 142.857 = 428.571. Die jeweiligen Produkte würden den Brüchen  bis
bis 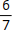 entsprechen.
entsprechen.
Multiplizierst du die zyklische Zahl mit der Generatorzahl (die ursprüngliche Zahl, aus der du den Kehrwert gebildet hast) erhältst du als Produkt nur Neuner. So ergibt das Produkt aus 7 ⋅ 142.857 die Ziffernfolge 999.999, was dem Bruch 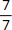 entspricht.
entspricht.
| Eigenschaften der zyklischen Zahl 142.857: | So sieht's aus: |
|---|---|
|
1.
Bilde den Kehrwert von 7 (ein Siebtel; |
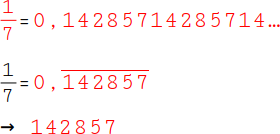 |
|
2.
Multipliziere 142.857 mit 2: 142.857 · 2 = 285.714. |
142857·2 =285714 |
|
3.
Multipliziere 142.857 mit 3: 142.857 · 3 = 428.571. |
142857·3 =428571 |
|
4.
Multipliziere 142.857 mit 4: 142.857 · 4 = 571.428. |
142857·4 =571428 |
|
5.
Multipliziere 142.857 mit 5: 142.857 · 5 = 714.285. |
142857·5 =714285 |
|
6.
Multipliziere 142.857 mit 6: 142.857 · 6 = 857.142. |
142857·6 =857142 |
|
7.
Multipliziere 142.857 mit der Generatorzahl 7: 142.857 · 7 = 999.999. |
142857·7 =999999 |
Weitere zyklischen Zahlen sind:
- 0588235294117647 (16-stellig, erzeugt aus dem Kehrwert von 17)
- 052631578947368421 (18-stellig, erzeugt aus dem Kehrwert von 19)
- 0434782608695652173913 (22-stellig, erzeugt aus dem Kehrwert von 23)
- 0344827586206896551724137931 (28-stellig, erzeugt aus dem Kehrwert von 29)
Eine zyklische Zahl ist eine n-stellige natürliche Zahl. Wird sie mit einer natürlichen Zahl von 1 bis n multipliziert, so besteht das Produkt wieder aus den gleichen Ziffern wie die Ausgangszahl in derselben zyklischen Reihenfolge.
Das könnte dich auch interessieren
Du hast einen Fehler gefunden oder möchtest uns eine Rückmeldung zu diesem Eintrag geben? Rückmeldung geben
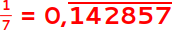 . Diese 6 Ziffern bilden die zyklische Zahl 142.857, mit der wir nur rechnen werden.
. Diese 6 Ziffern bilden die zyklische Zahl 142.857, mit der wir nur rechnen werden.