Konstruktion eines Umkreises um ein Dreieck

Ein Umkreis ist ein Element der Geometrie und stellt dabei ein Kreisbogen dar. Auf ihm liegen alle Eckpunkte einer bestimmten geometrischen Fläche, beispielsweise ein Dreieck oder ein Rechteck.

Um einen Umkreis zu konstruieren, zeichnest du die Mittelsenkrechten der Seitenlinien ein (diese stehen im 90°-Winkel in der Mitte der Seitenlinie). An dem Punkt, an dem sich alle Mittelsenkrechten aller Seitenlinien schneiden, sitzt der Mittelpunkt des Umkreises.

Du sollst einen Umkreis konstruieren, auf dem alle Eckpunkte eines Dreiecks liegen. Zum Konstruieren eines Umkreises benötigst du deinen Zirkel. Da du aber zuerst noch Vorarbeit leisten musst, benötigst du noch deinen Bleistift sowie dein Lineal bzw. Geodreieck. Zuerst zeichnest du mindestens zwei Mittelsenkrechten ein. Dazu zeichnest du je einen Kreisbogen um die Enden einer Seite mit einem Radius, der größer als die Hälfte der Seite ist. Zeichne dann durch den Schnittpunkt der beiden Kreisbögen die Mittelsenkrechten. Die Mittelsenkrechten schneiden sich in einem Punkt, der den Mittelpunkt des Umkreises darstellt. Stelle den Zirkel so ein, dass die Spitze im Mittelpunkt steht und das andere Ende des Zirkels zu einem Eckpunkt reicht. Zeichne nun einen Kreisbogen um diesen Mittelpunkt, der durch alle Eckpunkte geht.

So konstruierst du einen Umkreis:	So sieht's aus:
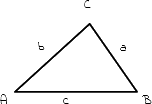
1. Von diesem Dreieck soll der Umkreis konstruiert werden. Dazu musst du mindestens zwei Mittelsenkrechten einzeichnen, um den Mittelpunkt des Umkreises zu finden.
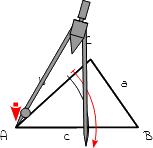
2. Zeichne zuerst die Mittelsenkrechte der Seite c. Steche mit dem Zirkel in den Eckpunkt A ein. Zeichne um ihn einen Kreisbogen mit einem beliebigen Radius, der größer als die Hälfte der Seite c ist.
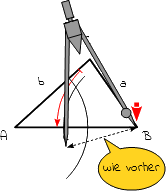
3. Verändere am Radius des Zirkels nichts! Steche ihn nun in den Punkt B ein. Zeichne einen weiteren Kreisbogen um ihn mit dem gleichen Radius vor vorher.
4. Zeichne nun die Mittelsenkrechte entlang dem Geodreieck ein. Sie geht durch die Schnittpunkte der beiden Kreisbögen.
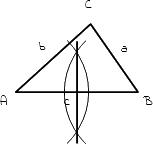
5. Du hast nun die Mittelsenkrechte der Seite c gezeichnet. Da du mindestens zwei Mittelsenkrechten benötigst, zeichnest du als nächstes die Mittelsenkrechte der Seite b.
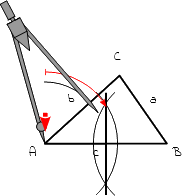
6. Steche dazu mit dem Zirkel wieder in den Eckpunkt A ein. Zeichne um ihn einen Kreisbogen mit einem beliebigen Radius, der größer als die Hälfte der Seite b ist.
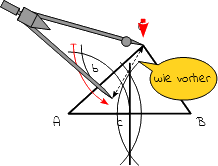
7. Verändere am Radius des Zirkels nichts! Steche ihn nun in den Punkt C ein. Zeichne einen weiteren Kreisbogen um ihn mit dem gleichen Radius vor vorher.
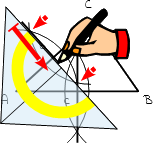
8. Zeichne nun die Mittelsenkrechte entlang dem Geodreieck ein. Sie geht durch die Schnittpunkte der beiden Kreisbögen.
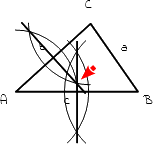
9. Du hast nun die Mittelsenkrechte der Seite b gezeichnet. Bereits jetzt siehst du, dass sich beide Mittelsenkrechten in einem Punkt schneiden. Dieser Punkt ist der Mittelpunkt des späteren Umkreises. Wenn du magst, kannst du noch die Mittelsenkrechte der Seite a einzeichnen. Auch sie muss durch den gemeinsamen Schnittpunkt gehen.
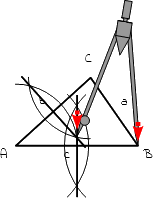
10. Steche mit dem Zirkel in den Schnittpunkt der Mittelsenkrechten ein. Stelle den Zirkel so ein, dass das andere Ende des Zirkels bis in einen Eckpunkt (beispielsweise Eckpunk B) reicht.
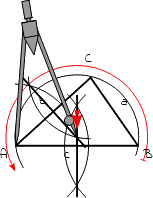
11. Zeichne um den Mittelpunkt einen Kreisbogen mit dem vorher eingestellten Radius. Der Kreisbogen muss durch alle drei Eckpunkte gehen.
12. Fertig - du hast nun den Umkreis konstruiert, der durch alle Eckpunkte des Dreiecks geht.