Delisches Problem
Der Legende nach befragten die Bewohner der Insel Delos (Griechenland) während einer Pestepidemie ihr Orakel um Rat. Das forderte sie auf, das Volumen des würfelförmigen Altars im Tempel des Apollon zu verdoppeln. Für damalige Mathematiker bedeutete dies, dass die Seitenlänge eines Würfels mit dem doppelten Volumen unter ausschließlicher Verwendung von Zirkel und Lineal konstruiert werden sollte.
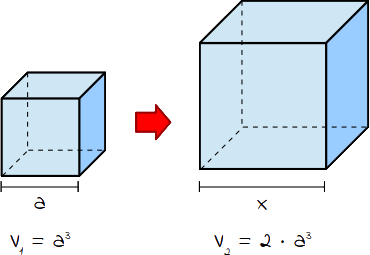
Der linke Würfel hat die Seitenlänge a, daher beträgt sein Volumen a³ (a · a · a). Der rechte Würfel hat das doppelte Volumen also 2 · a³, mit der noch unbekannten Seitenlänge x. Aus dem doppeltem Volumen kannst du nun die gesuchte Seite x berechnen. Dazu musst du nur die 3. Wurzel aus dem Volumen ziehen. Du erhältst als neue Seitenlänge x = ∛(2 · a³).
Dieses mathematische Problem der Würfelverdopplung ist allein mit Lineal und Zirkel nicht zu lösen. Erst der Mathematiker Évariste Galois (1811–1832) wies nach, dass das delische Problem zeichnerisch unlösbar ist. Grund dafür ist, dass die irrationale Zahl ∛(2 · a³) nicht durch ganze Zahlen, die vier Grundrechenarten und Quadratwurzeln, ausgedrückt werden kann.
| So könntest du es rechnerisch lösen: | So sieht's aus: |
|---|---|
| Du sollst das Volumen eines Würfels verdoppeln. | |
|
1.
Nehmen wir an, der linke Würfel hätte eine Seitenlänge von 10 cm. Damit beträgt sein Volumen (V1): 10 cm · 10 cm · 10 cm = 1.000 cm³. |
V1=a³ V1=(10cm)³=1000cm³ |
|
2.
Der rechte Würfel hätte dann das Doppelte davon (V2): 1.000 cm³ · 2 = 2.000 cm³. |
V2=2·V1 V2=2·1000cm³=2000cm³ |
|
3.
Aus diesem neuen Volumen musst du nun die 3. Wurzel ziehen, um die unbekannte Seitenlänge x zu erhalten: ∛(2.000cm³) = 12,5992105 cm. |
V2=x³ x=∛(V2)=∛(2.000cm³) x=12,5992105cm |
|
4.
Die Seitenlänge des neuen Würfels beträgt 12,5992105 cm. |
x=12,5992105cm |
Du siehst, aus einer eigentlich ganz einfach klingenden Aufgabe ist ein unlösbares Problem geworden…
Das könnte dich auch interessieren
Du hast einen Fehler gefunden oder möchtest uns eine Rückmeldung zu diesem Eintrag geben? Rückmeldung geben