Punktspiegelung

Wenn du in einen Spiegel schaust, dann siehst du dich selbst. Alles was du in diesem Spiegel siehst, nennt man Spiegelbild. So einen Spiegel gibt es nicht nur im Badezimmer oder im Flur, sondern auch in der Mathematik bzw. in der Geometrie. Hier schauen geometrische Objekte wie Flächen oder Körper in einen Spiegel und sehen sich wieder, nur umgekehrt - spiegelverkehrt eben.

Bei der Punktspiegelung erfolgt die Spiegelung geometrischer Objekte anhand einem einzigen Punkt, der auch als Zentrum Z oder Spiegelpunkt bezeichnet wird. Dieser Spiegelpunkt ordnet jedem Punkt des Objektes einen Spiegelbildpunkt zu, der zur Kennzeichnung einen kleinen hochgestellten Strich bekommt. So ist der Punkt A‘ der gespiegelte Punkt A.

Das Zentrum Z halbiert die Verbindungsstrecke zwischen dem ursprünglichen und dem gespiegelten Punkt. Das bedeutet, dass der ursprüngliche Punkt die gleiche Entfernung zum Spiegelpunkt hat, wie der gespiegelte Punkt.

Das gespiegelte Objekt ist bei der Punktspiegelung geraden-, längen- und winkeltreu, es entspricht in allem Abmessungen dem ursprünglichen Objekt. Daher sind beide kongruent (deckungsgleich).

Erfolgt die Punktspiegelung nur in der Ebene, so bewirkt sie eine Drehung des Objektes um 180°. Es ist anschließend spiegelverkehrt, bzw. steht auf dem Kopf.

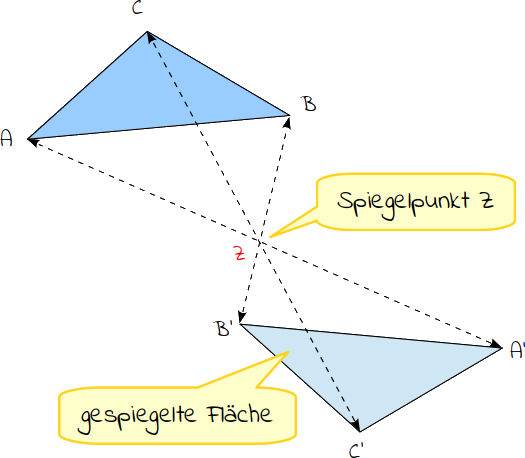
Um einen gespiegelten Punkt zu erhalten, wird eine Linie vom Punkt weit durch den Spiegelpunkt gezeichnet. Nun wird der Abstand zwischen beiden Punkten abgemessen. Diese Entfernung wird nun auf der anderen Seite des Spiegelpunktes eingezeichnet. Am Ende dieser Strecke befindet sich der Spiegelpunkt. Dabei wird die Verbindungsstrecke zwischen den beiden Punkten vom Spiegelpunkt halbiert. Dies kannst du auch mit einem Zirkel erledigen: Steche die Spitze in den Spiegelpunkt. Stelle den Zirkel so ein, dass die Mine bis in den Eckpunkt reicht. Zeichne nun einen Kreisbogen. Am Schnittpunkt zwischen Kreisbogen und Linie befindet sich der Spiegelpunkt. Sind alle Punkte gespiegelt, werden die gespiegelten Punkte wieder miteinander verbunden. Die neu entstandene Fläche entspricht in allen Maßen der Ausgangsfläche, sie sind beide kongruent (deckungsgleich).

So spiegelst du ein Objekt an einem Punkt:	So sieht's aus:
Dieses Dreieck ABC soll an der Spiegelachse (gestrichelt) gespiegelt werden.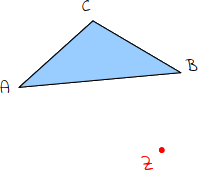
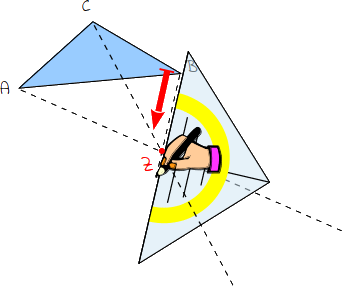
1. Zeichne eine senkrechte Linie von jedem Eckpunkt weit durch den Spiegelpunkt.
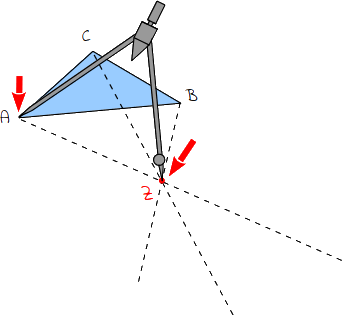
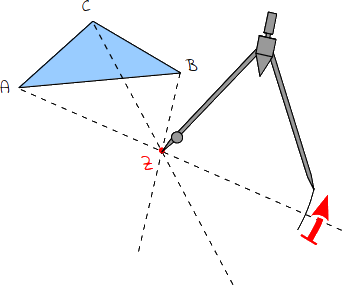
2. Steche die Spitze in den Spiegelpunkt. Stelle den Zirkel so ein, dass die Mine bis in den Eckpunkt reicht.
3. Zeichne nun einen kurzen Kreisbogen. Wiederhole dies bei allen Punkten. Stelle dabei den Zirkel jedes Mal neu ein!
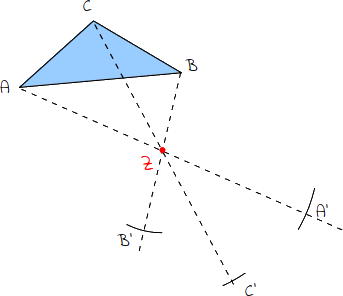
4. Am Schnittpunkt zwischen Kreisbogen und Linie befindet sich der Spiegelpunkt. Dieser wird mit einem kleinen hochgestellten Strich gekennzeichnet. So ist der Punkt A‘ der gespiegelte Punkt A.
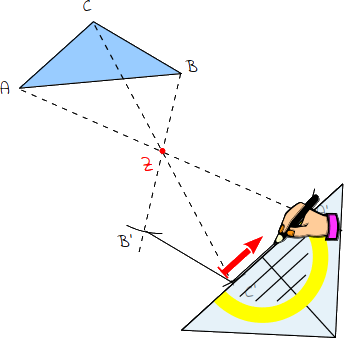
5. Sind alle Punkte gespiegelt, werden die gespiegelten Punkte wieder miteinander verbunden.
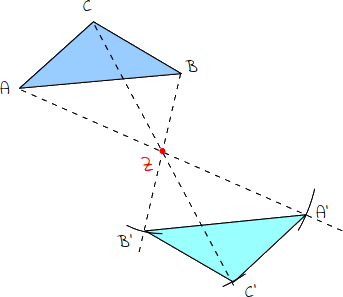
6. Die neu entstandene Fläche entspricht in allen Maßen der Ausgangsfläche, sie sind beide kongruent.

Bei der Punktspiegelung erfolgt die Spiegelung anhand eines einzigen Punktes, dem Spiegelpunkt. Er ordnet jedem Punkt des Objektes einen Spiegelbildpunkt zu.