Strahlensatz
Der Strahlensatz gehört zu den wichtigsten Aussagen der Geometrie. Er macht sich die Streckenverhältnissen zwischen bestimmten Stecken zunutze und ermöglicht so unbekannte Streckenlängen zu berechnen. Die Anwendung des Strahlensatzes soll auf den antiken griechischen Mathematiker Thales von Milet (624-547 v. Chr.) zurückgehen. Er hatte mit Hilfe eines Stabes durch Messung der Schattenlänge die Höhe der ägyptischen Cheopspyramide (heute etwa 138,75 m) ermittelt: Zunächst maß er die Seitenlänge der Pyramide und anschließend die Länge ihres Schattens. Anschließend steckte er einen Holzstab senkrecht in den Boden, vermaß seine Höhe und seine Schattenlänge. Durch die Verhältnisse aus der Länge des Schattenstabes zu seinem Schatten konnte der mit der Schattenlänge der Pyramide ihre Höhe bestimmen.
Damit du den Strahlensatz anwenden kannst, benötigst du bestimmte Voraussetzungen: du benötigst zwei Geraden (g und h), die sich in einem Punkt (Z) schneiden. Des Weiteren schneiden die beiden Geraden zwei parallel verlaufende Geraden (p1 und p2). Als weitere Bedingung darf keine der parallelen Geraden durch den Punkt Z gehen. Liegt der Punkt Z außerhalb der beiden parallelen Geraden, so spricht man auch von einer »V-Figur« (linke Abbildung), liegt der Punkt Z innerhalb der beiden parallelen Geraden, so spricht man auch von einer »X-Figur« (rechte Abbildung).
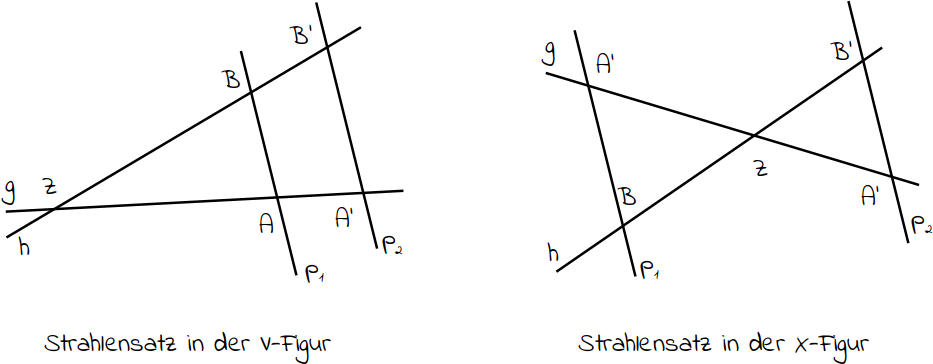
| Möglichkeiten beim Strahlensatz: | So sieht's aus: |
|---|---|
|
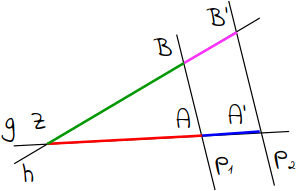
1.
Es verhalten sich je zwei Strecken auf der Geraden g so zueinander wie die entsprechenden Abschnitte auf der anderen Geraden h: ZA zu AA' wie ZB zu BB'. |
 |
|
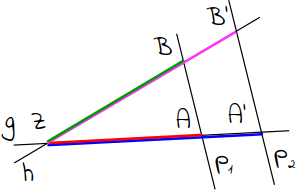
2.
Es verhalten sich je zwei Strecken auf der Geraden g so zueinander wie die entsprechenden Abschnitte auf der anderen Geraden h: ZA zu ZA' wie ZB zu ZB'. |
 |
|
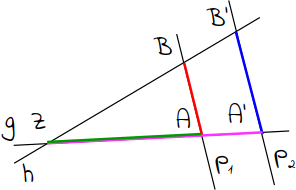
3.
Es verhalten sich die Strecken auf den Parallelen p1 und p2 so zueinander wie die entsprechenden vom Punkt Z ausgehenden Abschnitte auf der Geraden g: AB zu A'B' wie ZA zu ZA'. |
 |
|
4.
Es verhalten sich die Strecken auf den Parallelen p1 und p2 so zueinander wie die entsprechenden vom Punkt Z ausgehenden Abschnitte auf der Geraden h: A'B' zu AB wie ZB' zu ZB. |
 |
Über den Strahlensatz kannst du dir nun unbekannte Streckenlängen berechnen. Überlege dir zuerst, welche Möglichkeit aus der oberen Tabelle auf deine Aufgabe zutrifft. Setze anschließend die gegebenen Werte in die Formel ein. Eine Besonderheit bei der Berechnung mit dem Strahlensatz ist das Kreuzprodukt: Die beiden Brüche werden dabei über Kreuz multipliziert. Das bedeutet, du multiplizierst den Zähler des ersten Bruches mit dem Nenner des zweiten Bruches und den Nenner des ersten Bruches mit dem Zähler des zweiten Bruches. Stelle nun die Formel so um, dass du den fehlenden Wert berechnen kannst.
| So sieht's aus: | |
|---|---|
| Du sollst die Länge der Strecke A'B' berechnen. Dazu sind folgende Längen gegeben: ZA = 6 cm, ZA' = 9 cm und AB = 2 cm. | 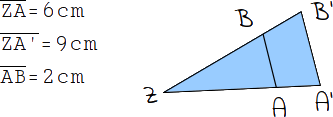 |
|
1.
Zuerst musst du dir überlegen, welche Möglichkeit aus der oberen Tabelle in Frage kommt. In unserem Beispiel passt nur die 3. Möglichkeit: AB zu A'B' wie ZA zu ZA'. |
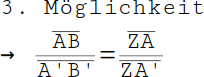 |
|
2.
Setze nun die gegebenen Werte in die Formel ein: AB = 2 cm, ZA = 6 cm und ZA' = 9 cm. |
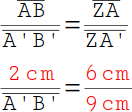 |
|
3.
Die beiden Brüche werden über Kreuz multipliziert. Multipliziere den Zähler des ersten Bruches mit dem Nenner des zweiten Bruches und den Nenner des ersten Bruches mit dem Zähler des zweiten Bruches. Zum Schluss drehen wir die Gleichung noch um. |
 |
|
4.
Nun müssen wir die Formel umstellen, um den Wert für A'B' zu berechnen. Dazu dividieren wir die Gleichung mit 6 cm. |
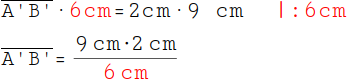 |
|
5.
Berechne den Zähler des Bruches: 9 cm · 2 cm = 18 cm². Beachte, dass du ein cm² erhältst, da cm · cm = cm²). Dies stört uns aber nicht weiter. |
 |
|
6.
Rechne nun den Bruch aus: 18 cm² : 2 cm = 3 cm. Das cm² löst sich durch die Division mit cm wieder in ein gewöhnliches cm auf. |
 |
|
7.
Dein Ergebnis lautet A'B' = 3 cm. |
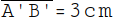 |
Über den Strahlensatz kannst du dir unbekannte Streckenlängen berechnen. Damit du ihn anwenden kannst, müssen jedoch bestimmte Voraussetzungen gegeben sein.
Das könnte dich auch interessieren
Du hast einen Fehler gefunden oder möchtest uns eine Rückmeldung zu diesem Eintrag geben? Rückmeldung geben
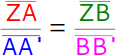 .
. .
.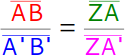 .
.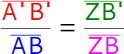 .
.