Umfang
Jede Fläche hat bestimmte Eigenschaften. Dazu gehört beispielsweise die Anzahl an Eckpunkte oder die Summe der Innenwinkel (Winkelsumme). Eine weitere Eigenschaft ergibt sich aus der Anzahl der einzelnen Seitenlinien. Auch aus diesen kannst du eine Summe bilden. Dazu addierst du einfach die Länge aller Seitenlinien zusammen. Den Wert, den du dann erhältst wird Umfang genannt. Da die Seitenlinien mit Längeneinheiten versehen sind, wird der Umfang auch als Längeneinheit (z. B. cm) angegeben.
Je nach Aussehen der Fläche musst du mehr oder weniger Seitenlinien addieren. Bei einem Dreieck sind es nur drei Werte, bei einem Achteck musst du eben acht Werte addieren.
u = a + b + c + …
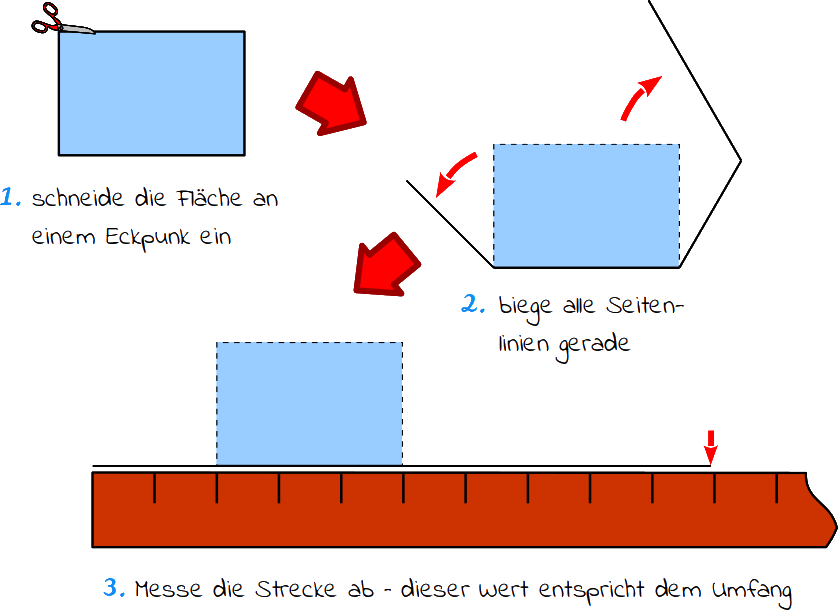
Bildlich kannst du dir das so vorstellen: Du trennst die Fläche an einem Eckpunkt auf, biegst alle Seitenlinien gerade und misst diese Stecke aus.
| So ermittelst du den Umfang einer Fläche: | So sieht's aus: |
|---|---|
| Du sollst den Umfang dieses allgemeinen Fünfecks berechnen. |  |
|
1.
Der Umfang ist die Summe aller Seitenlinien. Bei einem Fünfeck musst du daher fünf Seitenlinien addieren. Beginne bei einer beliebigen Seitenlinie. Wir beginnen mit der Seitenlinie ganz unten. Deine Rechnung beginnt mit: u = 10 cm + …. |
u=10cm+… |
|
2.
Addiere nun der Reihe nach die weiteren Seitenlinien dazu. Wir gehen dabei gegen den Uhrzeigersinn vor. Deine Rechnung ist inzwischen gewachsen und lautet nun: u = 10 cm + 5,5 cm + 8 cm…. |
u=10cm+5,5cm+8cm+… |
|
3.
Nun noch die letzte Seitenlinie hinzuaddieren und sind wir haben alle Seitenlinien verwendet. Unsere fertige Rechnung lautet nun: u = 10 cm + 5,5 cm + 8 cm + 8 cm + 3 cm. |
u=10cm+5,5cm+8cm+8cm+3cm |
|
4.
Löse nun die Addition: u = 10 cm + 5,5 cm + 8 cm + 8 cm + 3 cm = 34,5 cm. |
u=10cm+5,5cm+8cm+8cm+3cm u=34,5cm |
|
5.
Der Umfang des allgemeinen Fünfecks beträgt 34,5 cm. |
u=34,5cm |
Der Umkreis ist ein Kreis, auf dem sich alle Eckpunkte von bestimmten Flächen befinden.
Das könnte dich auch interessieren
Du hast einen Fehler gefunden oder möchtest uns eine Rückmeldung zu diesem Eintrag geben? Rückmeldung geben