archimedische Körper

Von den unzähligen Körpern, die es gibt, haben 13 Körper Seitenflächen, die regelmäßige Polygone (Vielecke) sind. Alle Ecken eines solchen Körpers verhalten sich zueinander völlig gleich. Dies wird auch als »Uniformität der Ecken« genannt und bedeutet: Zu jedem Eckpaar (Ecke 1 und Ecke 2) des Körpers ist es möglich, den Körper so zu drehen und zu spiegeln, dass die Ecke 1 dort zu liegen kommt, wo zuvor die Ecke 2 war und die beiden Positionen des Körpers vor und nach der Drehung nicht zu unterscheiden sind.

Diese Eigenschaft erfüllen auch die platonischen Körper, Prismen und Antiprismen. Dabei gehören die archimedischen Körper keiner dieser drei Gruppen an. Diese speziellen Körper wurden nach dem großen griechischen Mathematiker Archimedes benannt, der sie vermutlich alle entdeckte.

Darüber hinaus haben alle Kanten eines archimedischen Körpers die gleiche Länge. Jeder archimedische Körper kann durch Abstumpfen, also dem Wegschneiden von Ecken, aus einem platonischen Körper erzeugt werden. Dies führt auch bei vielen Körpern zu ihrem Namen.

Name:	Aussehen:	Flächen:	Kanten:	Ecken:
Tetraederstumpf		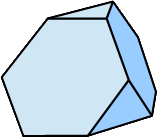8 (4 gleichseitige Dreiecke, 4 regelmäßige Sechsecke)	18	12
Kuboktaeder		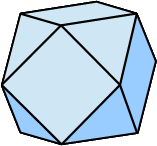14 (8 gleichseitige Dreiecke, 6 Quadrate)	24	12
Hexaederstumpf		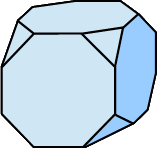14 (8 gleichseitige Dreiecke, 6 regelmäßige Achtecke)	36	24
Oktaederstumpf		14 (6 Quadrate, 8 regelmäßige Sechsecke)	36	24
Rhombenkuboktaeder		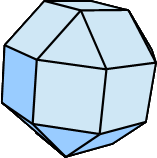26 (8 gleichseitige Dreiecke, 18 Quadrate)	48	24
Kuboktaederstumpf		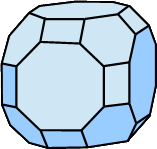26 (12 Quadrate, 8 regelmäßige Sechsecke, 6 regelmäßige Achtecke)	72	48
Ikosidodekaeder		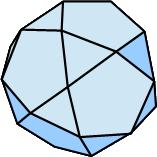32 (20 gleichseitige Dreiecke, 12 regelmäßige Fünfecke)	60	30
Dodekaederstumpf		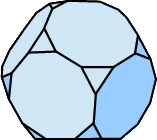32 (20 gleichseitige Dreiecke, 12 regelmäßige Zehnecke)	90	60
Ikosaederstumpf		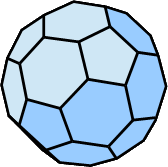32 (12 regelmäßige Fünfecke, 20 regelmäßige Sechsecke)	90	60
abgeschrägtes Hexaeder		38 (32 gleichseitige Dreiecke, 6 regelmäßige Quadrate)	60	24
Rhombenikosidodekaeder		62 (20 gleichseitige Dreiecke, 30 regelmäßige Quadrate, 12 regelmäßige Fünfecke)	120	60
Ikosidodekaederstumpf		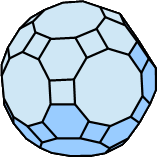62 (30 Quadrate, 20 regelmäßige Sechsecke, 12 regelmäßige Zehnecke)	180	120
abgeschrägtes Dodekaeder		92 (80 gleichseitige Dreiecke, 12 regelmäßige Fünfecke)	150	60

Die archimedischen Körper besitzen Seitenflächen, die regelmäßige Polygone sind, erfüllen die »Uniformität der Ecken«, sind aber weder platonische Körper, Prismen noch Antiprismen. Es gibt nur 13 Körper, auf die diese Eigenschaften zutreffen.