Definitionsmenge (Ausschluss)
Weißt du was eine Funktion ist? Das ist ein mathematischer Ausdruck, bei dem ein bestimmtes Verhältnis herrscht. Eine Funktion enthält neben richtigen Zahlen auch einen Platzhalter, für den du beliebige Zahlen einsetzen kannst. Dieser wird meistens mit einem x dargestellt. Nehmen wir als Beispiel eine sehr einfache Funktion: f(x) = 2 · x. Du sollst also anstelle von x eine Zahl einsetzen und sie verdoppeln (2 · x). Das Verhältnis besteht also darin, dass das Ergebnis stets doppelt so groß ist wie deine eingesetzte Zahl.
Nun kannst du anstelle von Zahlen auch Brüche bzw. Bruchterme in deiner Funktion haben. Besonders aufpassen musst du bei Bruchtermen, wenn du die unbekannte Zahl (das x) in einem der Nenner stehen hast. Wie du sicherlich weißt, darf in der Mathematik der Nenner nie 0 (Null) sein, da du nicht durch 0 dividieren darfst. Nehmen wir mal an, in einem Nenner steht (2 · x + 6). Zugelassen wären alle ganzen Zahlen (ℤ), also alle positiven und negativen Zahlen ohne Komma. Setzt du jetzt anstelle des x den Wert (-3), so bekommt dein Nenner den verbotenen Wert 0. Du musst also irgendwie verhindern, dass jemand den Wert -3 einsetzen kann. Dies machst du über die so genannte Definitionsmenge.
Die Definitionsmenge beinhaltet nämlich alle Zahlen, für die eine Funktion definiert ist. Das heißt also, es sind alle Zahlen zugelassen, die in der Definitionsmenge stehen. Nun kannst auch das Gegenteil machen: Du kannst bestimme Zahlen aus der Definitionsmenge ausschließen. Sie sind dann für diese Funktion nicht zugelassen. Du darfst sie also nicht verwenden. Diese ausgeschlossenen Zahlen schreibst du hinter den zulässigen Zahlen getrennt durch einen nach links geneigten Schrägstrich »\«. Für das obige Beispiel wären alle ganzen Zahlen ℤ zugelassen, bis auf den Wert -3. Gelesen wird dies: „Die Definitionsmenge enthält alle Elemente der Menge der ganzen Zahlen ohne das Element -3“:
D = ℤ \ {-3}
| Daher sind Elemente ausgeschlossen: | So sieht's aus: |
|---|---|
| Du sollst die Definitionsmenge dieser Funktion bestimmen. Zugelassen sind alle Elemente der Menge der ganzen Zahlen. |  |
|
1.
Wichtig ist nur der Nenner in der Funktion, daher betrachten wir ihn uns einmal genauer: 2 · x + 6. |
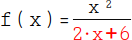 |
|
2.
Wir setzten nun anstelle des x den Wert -3 ein. |
 |
|
3.
Wir berechnen zuerst die Klammer: (2 · (-3)) = -6. |
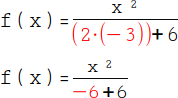 |
|
4.
Wir berechnen anschließend den Nenner: -6 + 6 = 0. Wir erhalten als Ergebnis den verbotenen Wert von 0, da Divisionen durch 0 nicht zulässig sind. |
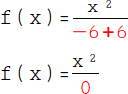 |
|
5.
Du darfst also alle Zahlen einsetzen bis auf die -3. Daher musst du sie aus der Definitionsmenge ausschließen. Du erweiterst die Definition D = ℤ um den Ausschlusszusatz: \ {–3}. Deine neue Definition lautet: D=ℤ\{–3}. Gelesen wird dies: „Die Definitionsmenge enthält alle Elemente der Menge der ganzen Zahlen ohne das Element -3“. |
D=ℤ\{–3} |
Die Definitionsmenge beinhaltet die Zahlen, für die eine Funktion definiert ist. Stelle dir einfach folgende Frage: „Welche Zahlen darf ich in die Funktion einsetzen?“. Der Zusatz \{…} enthält Zahlen, die nicht zulassen sind.
Das könnte dich auch interessieren
Du hast einen Fehler gefunden oder möchtest uns eine Rückmeldung zu diesem Eintrag geben? Rückmeldung geben