Bruchgleichung lösen
Eine Gleichung ist ein mathematischer Ausdruck. Wie der Name Gleichung schon sagt, muss bei ihm etwas gleich sein. Sie besteht aus zwei Teilrechnungen, die mit einem Gleichheitszeichen (=) verbunden sind. Daher müssen beide Teilrechnungen stets den gleichen Wert haben. Wenn du beide Teilrechnungen ausrechnest, so müssen sie jeweils das gleiche Ergebnis haben. Die einfachste Gleichung ist eine gewöhnliche Rechnung: 2 + 2 = 4. Links und rechts des Gleichheitszeichen steht jeweils der gleiche Wert, nämlich 4.
Oftmals enthalten solche Gleichungen auch eine oder auch mehrere Unbekannte, deren Wert du am Anfang noch nicht kennst. Diese wird meistens mit einem x dargestellt. Nehmen wir als Beispiel eine sehr einfache Gleichung: 3 + x = 2 + 5. Du sollst also anstelle von x eine Zahl einsetzen und sie mit 3 addieren. Der Wert dieser linken Addition muss dann den gleichen Wert haben wie die Addition auf der rechten Seite, nämlich 7. Du müsstest jetzt die Gleichung umstellen und würdest dann für x den Wert 4 herausbekommen. Denn nur mit x = 4 stimmt die Gleichung.
Nun kannst du anstelle von Zahlen auch Brüche bzw. Bruchterme in deiner Gleichung haben. Besonders aufpassen musst du bei Bruchtermen, wenn du die Unbekannte (das x) in einem der Nenner stehen hast. Wie du sicherlich weißt, darf in der Mathematik der Nenner nie 0 (Null) sein, da du nicht durch 0 dividieren darfst. Nehmen wir mal an, in einem Nenner steht (2 - x). Zugelassen wären alle ganzen Zahlen (ℤ), also alle positiven und negativen Zahlen ohne Komma. Setzt du jetzt anstelle des x den Wert 2, so bekommt dein Nenner den verbotenen Wert 0, da 2 - 2 = 0. Du musst also irgendwie verhindern, dass jemand den Wert 2 einsetzen kann. Dies machst du über die so genannte Definitionsmenge.
| So berechnest du eine Bruchgleichung: | So sieht's aus: |
|---|---|
| Du sollst diese Bruchgleichung berechnen. | 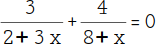 |
|
1.
Zuerst musst du die Definitionsmenge bestimmen, da du sogar mehrmals eine Unbekannte (x) im Nenner hast. |
D=? |
|
2.
Wir schauen uns den ersten Nenner an. Gesucht ist hier eine Zahl, die mit 3 multipliziert und anschließend mit 2 addiert 0 ergibt (2 + 3 · x = 0). Wir stellen um und erhalten : x = - |
2+3x=0 |-2 3x=-2 |:3 3x:3=-2:3 x=-  |
|
3.
Wir schauen uns den zweiten Nenner an. Gesucht ist hier eine Zahl, die mit 8 addiert 0 ergibt (8 + x = 0). Wir stellen um und erhalten : x = -8, da 8 + (-8) = 0. |
8+x=0 |-8 x=-8 |
|
4.
Du darfst also alle Zahlen einsetzen bis auf die - |
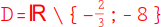 |
|
5.
Als nächster Schritt musst du den Hauptnenner bestimmen, damit die ganzen Brüche wegkommen. Zerlege dazu die Nenner in ihre Bestandteile, was bei unseren Brüchen jedoch nicht geht. Daher ist unser Hauptnenner das Produkt aus beiden Nennern: (2 + 3x) · (8 + x). |
2+3x → 2+3x 8+x → 8+x → HN: (2+3x)·(8+x) |
|
6.
Erweitere nun jeden Nenner auf den Hauptnenner. Beim ersten Bruch fehlt noch (8 + x), um auf den Hauptnenner zu kommen (die (2 + 3x) hast du ja bereits). Erweitere ihn also mit (8 + x). |
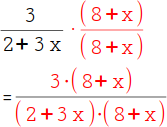 |
|
7.
Multipliziere die Klammer im Zähler aus. Multipliziere dazu die Zahl vor der Klammer mit jeder Zahl in der Klammer: 3 · 8 = 24 und 3 · x = 3x. |
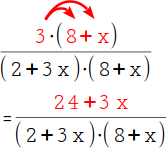 |
|
8.
Multipliziere im Nenner die erste Zahl in der ersten Klammer mit beiden Zahlen in der zweiten Klammer: 2 · 8 = 16 und 2 · x = 2x. |
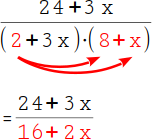 |
|
9.
Multipliziere im Nenner auch die zweite Zahl in der ersten Klammer mit beiden Zahlen in der zweiten Klammer: 3x · 8 = 24x und 3x · x = 3x². |
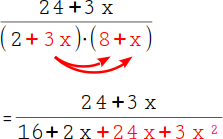 |
|
10.
Fasse nun die Zahlen in Nenner zusammen: 2x + 24x = 26x. Damit wäre der erste Nenner fertig. |
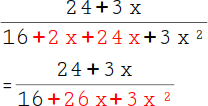 |
|
11.
Beim zweiten Bruch fehlt noch (2 + 3x), um auf den Hauptnenner zu kommen (die (8 + x) hast du ja bereits). Erweitere ihn also mit (2 + 3x). |
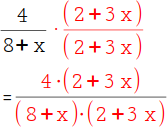 |
|
12.
Multipliziere die Klammer im Zähler aus. Multipliziere dazu die Zahl vor der Klammer mit jeder Zahl in der Klammer: 4 · 2 = 8 und 4 · 3x = 12x. |
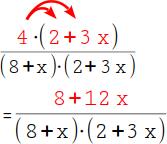 |
|
13.
Multipliziere im Nenner die erste Zahl in der ersten Klammer mit beiden Zahlen in der zweiten Klammer: 8 · 2 = 16 und 8 · 3x = 24x. |
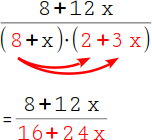 |
|
14.
Multipliziere im Nenner auch die zweite Zahl in der ersten Klammer mit beiden Zahlen in der zweiten Klammer: x · 2 = 2x und x · 3x = 3x². |
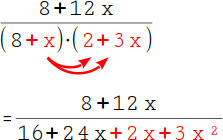 |
|
15.
Fasse nun die Zahlen im Nenner zusammen: 2x + 24x = 26x. Damit wäre der zweite Nenner auch fertig. |
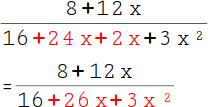 |
|
16.
Die beiden Brüche sind gleichnamig, du kannst sie addieren. Schreibe alles auf einen Bruchstich: 24 + 3x + 8 + 12x. Der Nenner (16 + 26x + 3x²) wird beibehalten. |
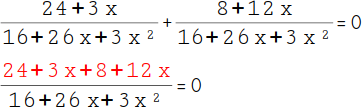 |
|
17.
Fasse nun die Zahlen zusammen. Zuerst die beiden Zahlen ohne Unbekannte: 24 + 8 = 32. |
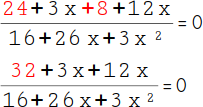 |
|
18.
Fasse anschließend die Zahlen mit der Unbekannten zusammen: 3x + 12x = 15x. |
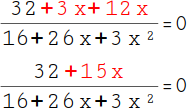 |
|
19.
Multipliziere nun auf beiden Seiten mit den Nenner (16 + 26x + 3x²), um den Bruch zu beseitigen. |
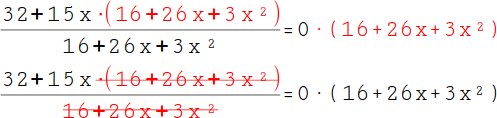 |
|
20.
Übrig bleibt noch eine Gleichung ohne Bruch: 32 + 15x = 0 · (16 + 26x + 3x²). |
32+15x=0·(16+26x+3x²) |
|
21.
Die rechte Seite ist schnell ausgerechnet: 0 · (16 + 26x + 3x²) = 0. |
 32+15x=0·(16+26x+3x²) 32+15x=0·(16+26x+3x²)32+15x=0 |
|
22.
Nun muss nur noch die 32 auf die andere Seite. Subtrahiere sie daher mit -32. |
32+15x=0 |-32 15x=-32 |
|
23.
Du hast nun 15x. Um den Wert für x zu erhalten, dividiere die Gleichung durch 15. |
15x=-32 |:15 15x:15=-32:15 |
|
24.
Dividiere nun die linke Seite, um 1 x zu erhalten: 15x : 15 = x. |
15x:15=-32:15 x=-32:15 |
|
25.
Dividiere die rechte Seite, um den x-Wert zu erhalten: -32 : 15 = - |
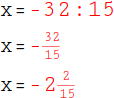 |
|
26.
Vergleiche nun deine Lösung (x-Wert) mit der Definitionsmenge. Unser Wert -2 |
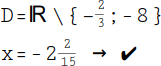 |
|
27.
Hast du deine Lösung mit der Definitionsmenge verglichen, gibst du sie in der Lösungsmenge L an: L = {-2 |
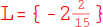 |
Eine Bruchgleichung ist eine Gleichung mit Brüchen. Aufpassen musst du, wenn im Nenner eine Unbekannte steht, da der Nenner nie den Wert 0 annehmen darf.
Das könnte dich auch interessieren
Du hast einen Fehler gefunden oder möchtest uns eine Rückmeldung zu diesem Eintrag geben? Rückmeldung geben

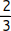 ) = 0.
) = 0. = -2
= -2 