Diskriminante

In einigen Gleichungen kommt das x nicht in einfacher Form, sondern als Quadrat (x²) vor. Solche Gleichungen werden daher auch quadratische Gleichungen genannt. Da hier das x zweimal vorkommt (als x · x), haben diese Gleichungen entweder zwei, eine oder keine Lösung. Wenn du die quadratische Gleichung in die Normalform (x² + px + q = 0) gebracht hast, kannst du deren Lösung durch Einsetzen in die Lösungsformel (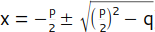) recht einfach berechnen. Die Anzahl der Lösungen (zwei, eine oder keine) ist dabei anhängig von der Diskriminante D. So wird der Ausdruck unter der Wurzel in der Lösungsformel bezeichnet, also . Das Wort Diskriminante stammt von dem lateinischen Wort »discriminare«, das »unterscheiden« bedeutet. Je nach Art ihres Wertes kannst du Aussagen über die Anzahl der Lösungen einer quadratischen Gleichung machen.

Ist der Wert der Diskriminante D () positiv, also größer als Null (D > 0), so hat deine Gleichung zwei Lösungen, nämlich x₁ und x₂: L = {x₁; x₂}. Ist der Wert der Diskriminante D neutral, also gleich Null (D = 0), so hat deine Gleichung eine Lösung: L = {x} (x₁ und x2 haben den gleichen Wert). Ist der Wert der Diskriminante D hingegen negativ, also kleiner als Null (D < 0), so hat deine Gleichung keine Lösung: L = {  }.

positive Diskriminante (D > 0) → Gleichung hat zwei Lösungen: L = {x₁; x₂}

neutrale Diskriminante (D = 0) → Gleichung hat eine Lösung: L = {x}

negative Diskriminante (D < 0) → Gleichung hat keine Lösung: L = {  }

Abhängig von der Diskriminante D kann eine Gleichung zwei (D > 0), eine (D = 0) oder auch keine (D < 0) Lösung haben.