Fallunterscheidungen (positive Diskriminante)
Eine Gleichung ist ein mathematischer Ausdruck. Wie der Name Gleichung schon sagt, muss bei ihm etwas gleich sein. Sie besteht aus zwei Teilrechnungen, die mit einem Gleichheitszeichen (=) verbunden sind. Daher müssen beide Teilrechnungen stets den gleichen Wert haben. Wenn du beide Teilrechnungen ausrechnest, so müssen sie jeweils das gleiche Ergebnis haben. Die einfachste Gleichung ist eine gewöhnliche Rechnung: 2 + 2 = 4. Links und rechts des Gleichheitszeichen steht jeweils der gleiche Wert, nämlich 4.
Oftmals enthalten solche Gleichungen auch einen Platzhalter, für den du beliebige Zahlen einsetzen kannst. Dieser wird meistens mit einem x dargestellt. Nehmen wir als Beispiel eine sehr einfache Gleichung: 3 + x = 2 + 5. Du sollst also anstelle von x eine Zahl einsetzen und sie mit 3 addieren. Der Wert dieser linken Addition muss dann den gleichen Wert haben wie die Addition auf der rechten Seite, nämlich 7. Du müsstest jetzt die Gleichung umstellen und würdest dann für x den Wert 4 herausbekommen. Denn nur mit x = 4 stimmt die Gleichung.
Nun gibt es Gleichungen, in denen das x nicht in einfacher Form, sondern als Quadrat (x²) vorkommt. Solche Gleichungen werden daher auch quadratische Gleichungen genannt. Da hier das x zweimal vorkommt (als x · x) haben diese Gleichungen entweder zwei, eine oder keine Lösung. Wenn du die quadratische Gleichung in die Normalform (x² + px + q = 0) gebracht hast, kannst du deren Lösung durch Einsetzen in die Lösungsformel ( ) recht einfach berechnen. Die Anzahl der Lösungen (zwei, eine oder keine) ist anhängig von der Diskriminante D. So wird der Ausdruck unter der Wurzel in der Lösungsformel bezeichnet, also
) recht einfach berechnen. Die Anzahl der Lösungen (zwei, eine oder keine) ist anhängig von der Diskriminante D. So wird der Ausdruck unter der Wurzel in der Lösungsformel bezeichnet, also 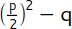 . Das Wort Diskriminante stammt von dem lateinischen Wort »discriminare«, das »unterscheiden« bedeutet. Je nach Art ihres Wertes kannst du Aussagen über die Anzahl der Lösungen einer quadratischen Gleichung machen.
. Das Wort Diskriminante stammt von dem lateinischen Wort »discriminare«, das »unterscheiden« bedeutet. Je nach Art ihres Wertes kannst du Aussagen über die Anzahl der Lösungen einer quadratischen Gleichung machen.
Ist der Wert der Diskriminante D (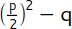 ) positiv, also größer als Null (D > 0), so hat deine Gleichung zwei Lösungen, nämlich x1 und x2: L = {x1; x2}.
) positiv, also größer als Null (D > 0), so hat deine Gleichung zwei Lösungen, nämlich x1 und x2: L = {x1; x2}.
positive Diskriminante (D > 0) → Gleichung hat zwei Lösungen: L = {x1; x2}
| Hier hat deine Gleichung zwei Lösung: | So sieht's aus: |
|---|---|
| Das hier ist deine quadratische Gleichung: | x²+2x-3=0 |
|
1.
Die Werte dieser Gleichung setzen wir nun in die Lösungsformel ein. Der Wert für p beträgt 2. Da wir aber |
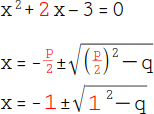 |
|
2.
Der Wert für q beträgt -3. Um die Klammer mit dem Minus davor aufzulösen, drehst du das Vorzeichen in der Klammer um. So ergibt sich ein Wert von +3. |
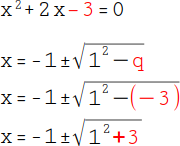 |
|
3.
Wir rechnen nun die Diskriminante D aus. Dazu wird zuerst einmal das Quadrat berechnet: 1² = 1. |
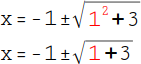 |
|
4.
Berechne beide Zahlen unter der Wurzel: 1 + 3 = 4. |
 |
|
5.
Die Diskriminante ist positiv (4), also hat unsere Gleichung zwei Lösungen (x1 und x2). |
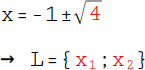 |
|
6.
Ziehe die Wurzel: √4 = 2. |
 |
|
7.
Nun können wir den Wert für x1 ausrechnen: -1 + 2 = 1. |
x1=–1+2 x1=1 |
|
8.
Gefolgt vom Wert für x2: -1 - 2 = -3. |
x2=–1-2 x2=-3 |
|
9.
Die Lösung für diese Gleichung lautet: L = {1; –3}. |
L={1;–3} |
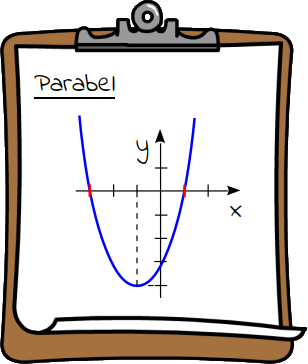
Das Schaubild der quadratischen Funktion (Parabel) schneidet die X-Achse in zwei Punkten: x1 = 1 und x2 = -3.
Diese zwei Punkte werden auch Nullstellen (Schnittpunkt mit der X-Achse) genannt
Das könnte dich auch interessieren
Du hast einen Fehler gefunden oder möchtest uns eine Rückmeldung zu diesem Eintrag geben? Rückmeldung geben
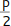 benötigen, halbieren wir den p-Wert:
benötigen, halbieren wir den p-Wert: