Flächeninhalt bei komplexen Flächen
Der Flächeneinheit ist der Inhalt einer Fläche. Er wird mit dem Großbuchstaben A abgekürzt (A wie englisch »area« und das bedeutet Fläche). Um den Flächeninhalt zu ermitteln, multiplizierst du die Länge der Fläche (a) mit der Breite der Fläche (b). Da du hierbei zwei Längeneinheiten multiplizierst, erhältst du das »Quadrat« der Längeneinheit. Dies kennzeichnest du mit einer hochgestellten Ziffer 2 (²). Aus den Längeneinheiten sind nun Flächeneinheiten geworden.
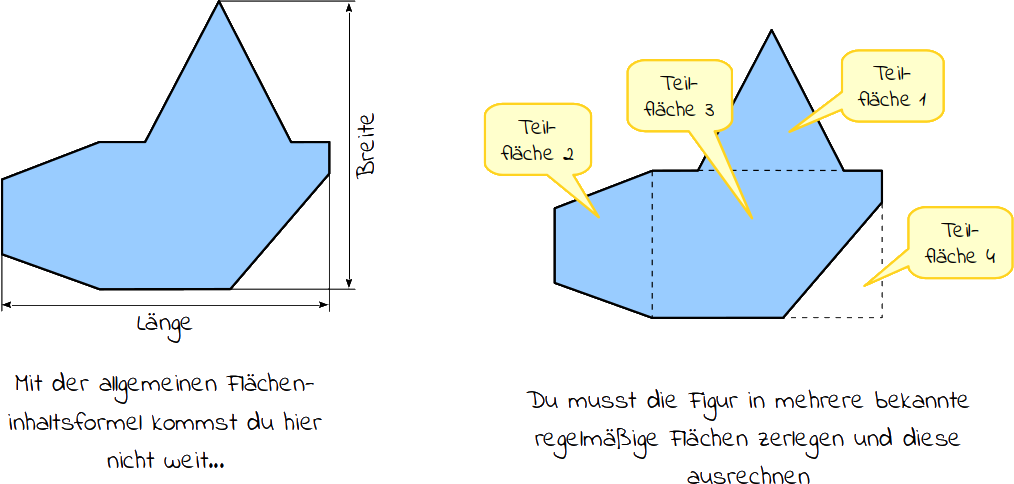
Bei regelmäßigen Flächen wie Rechteck oder Dreieck, ist es noch leicht, den Flächeninhalt zu berechnen. Wenn deine Fläche von den regelmäßigen Flächen abweicht, musst du die Fläche in geschickte Teilflächen aufteilen. Das bedeutet, du teilst die Fläche in bekannte geometrische regelmäßige Flächen wie Dreiecke, Rechtecke, Quadrate oder Trapeze auf. Anschließend berechnest du den Flächeninhalt der einzelnen Teilflächen. Je nach Aussehen der Fläche addierst bzw. subtrahierst du zum Schluss die einzelnen Teilflächeninhalte. Stell dir vor, du hast ein Quadrat, bei dem die rechte Seite halbrund gebogen ist. Du berechnest zuerst den Flächeninhalt des Quadrates und addierst den Flächeninhalt des Halbkreises dazu. Wenn du aber ein Rechteck mit einem runden Loch hast, so berechnest du zuerst den Flächeninhalt des Rechteck und subtrahierst den Flächeninhalt des Kreises. Wie du bei der unten abgebildeten Fläche vorgehst, zeigen wir dir nun.
| So ermittelst du den Flächeninhalt: | So sieht's aus: |
|---|---|
| Du sollst den Flächeninhalt dieser geometrischen Fläche ermitteln. |  |
|
1.
Mit der allgemeinen Flächeninhaltsformel (Länge · Breite) kommst du hier nicht weit. Du musst die Figur in mehrere bekannte regelmäßige Flächen zerlegen und diese ausrechnen. Die obere Spitze ist ein gleichschenkliges Dreieck, bei dem die linke und die rechte Seite gleich lang ist. Dieses Dreieck stellt deine Teilfläche 1 dar. |
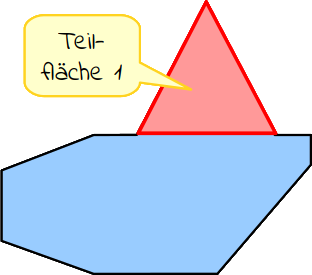 |
|
2.
Der linke Bereich der Fläche sieht aus wie ein gleichschenkliges Trapez. Gleichschenklig daher, weil die obere und die untere Seite gleich lang ist. Dieses Trapez stellt somit deine Teilfläche 2 dar. |
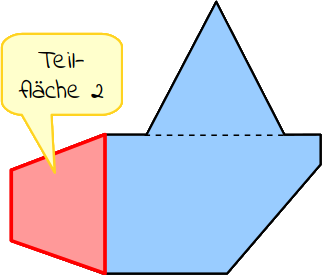 |
|
3.
Übrig bleibt dieses unregelmäßige Fünfeck, bei dem alle Seiten unterschiedlich lang sind. Mit dem kannst du nicht viel anfangen, da es für diese Fläche kleine allgemeine Formel gibt. Du musst diese Fläche also weiter aufteilen. |
 |
|
4.
Wenn wir diese Restfläche mal großzügig betrachten, so sieht sie doch wie ein großes Rechteck aus. Die untere rechte Ecke steht zwar über, aber das macht im Moment nichts. Dieses Rechteck wird deine Teilfläche 3. |
 |
|
5.
Das Rechteck (Teilfläche 3) ist ja eigentlich zu groß, da die untere rechte Ecke übersteht. Die überstehende Fläche sieht doch aus wie ein gleichschenkliches rechtwinkliges Dreieck. Gleichschenklig daher, weil die beiden kürzeren Seiten gleich lang sind. Der rechte Winkel ergibt sich aus dem Rechteck. Daher stellt dieses Dreieck deine Teilfläche 4 dar. |
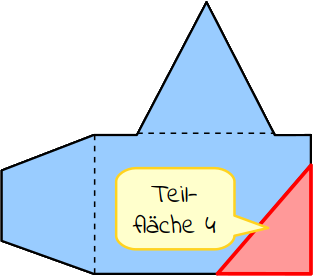 |
|
6.
Um den Flächeninhalt dieser Figur zu ermitteln, berechnest du zuerst alle Flächeninhalte der vier Teilflächen aus. Anschließend addierst du den Flächeninhalt aller grün eingefärbten Teilflächen (Teilfläche 1 bis 3). Zum Schluss subtrahierst du die rot eingefärbte Teilfläche 4, da sie ja übersteht und nicht zum Flächeninhalt der ursprünglichen Figur gehört. Du rechnest also AGesamt = ATeilfläche 1 + ATeilfläche 2 + ATeilfläche 3 – ATeilfläche 4. |
 |
Der Flächeninhalt von komplexeren geometrischen Figuren errechnest du, indem du die Fläche in regelmäßige Teilflächen zerlegt und deren Flächeninhalt berechnest. Anschließend addierst bzw. subtrahierst du die Teilflächeninhalte.
Das könnte dich auch interessieren
Du hast einen Fehler gefunden oder möchtest uns eine Rückmeldung zu diesem Eintrag geben? Rückmeldung geben