Menge der rationalen Zahlen

Die Menge der rationalen Zahlen ist eine Zahlenmenge. Sie erweitert den Zahlenbereich der ganzen Zahlen (alle positiven und negativen Zahlen ohne Nachkommastellen) so, dass du nun auch eingeschränkt dividieren kannst. Dies gelingt durch die Einführung von Nachkommastellen. Wenn du eine ganze Zahl durch eine beliebige ganze Zahl teilst (dividierst), gibt es keine ganze Zahl, die diesen Wert darstellen kann. Daher werden bei den Zahlen weitere Stellen eingeführt, die sogenannten Nachkommastellen oder Dezimale. Die neuen Zahlen mit den Nachkommastellen stehen zwischen den ganzen Zahlen, z. B. 1,6 oder -2,19.

Die Menge der rationalen Zahlen enthält alle positiven und negativen Zahlen mit Nachkommastellen (Dezimalen), die durch einen Bruch dargestellt werden können. Der Zähler (obere Zahl) und Nenner (untere Zahl) sind jeweils ganze Zahlen. Was eine rationale Zahl ausmacht, ist, dass sie Nachkommastellen (Dezimalen) hat. Diese sind jedoch nicht beliebig lang, sondern hören irgendwann auf oder sie setzen sich immer in der gleichen Reihenfolge fort. Solche Nachkommastellen werden periodische Dezimale genannt.

Das Formelzeichen für die Menge der ganzen Zahlen ist ein Q mit zwei Doppelstrichen an der Seite.

ℚ = {x | x = 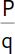∧ P ∈ ℤ; q ∈ ℤ*}

Den ersten Teil der oben stehenden „Hieroglyphen“ kennst du ja bereits: Das ℚ steht für die Menge der rationalen Zahlen. In der geschweiften Klammer hinter dem Gleichheitszeichen steht die Bedingung für die Elemente (x |), die sie erfüllen müssen: das Element (x) ist ein Bruch (x = 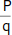). Das kleine Dach (∧) bedeutet »und«, also existiert noch eine weitere Bedingung: der Zähler des Bruches (P) ist eine Zahl aus der Menge der ganzen Zahlen (P ∈ ℤ), der Nenner des Bruches (q) ist eine Zahl aus der Menge der ganzen Zahlen (q ∈ ℤ). Das Sternchen hinter dem ℤ (ℤ*) bedeutet, dass du hier die Zahl 0 nicht verwenden darfst.

Die Menge der rationalen Zahlen ist eine Zahlenmenge. Sie enthält neben den positiven und negativen Zahlen alle Zahlen mit abbrechenden oder periodischen Nachkommastellen sowie die Zahl 0.