Permutation mit Wiederholung

Die Permutation gehört zur Kombinatorik, einem Teilgebiet der Mathematik. Der Name »permutare« ist lateinisch und bedeutet vertauschen. Sie beschreibt die Anordnung von Objekten in einer bestimmten Reihenfolge. Dürfen diese Objekte nicht mehrfach auftreten, spricht man von einer Permutation ohne Wiederholung.

Eine Permutation mit Wiederholung ist eine Anordnung von n Objekten, von denen manche nicht unterscheidbar sind. Sind genau k Objekte identisch, dann kannst du sie auf ihren Plätzen vertauschen, ohne dass sich dabei eine neue Reihenfolge ergibt. Auf diese Weise sind genau k! Anordnungen gleich. Die Anzahl der Permutationen von n Objekten, von denen k identisch sind, ist demnach durch die fallende Faktorielle

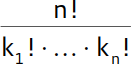
gegeben.

Nehmen wir als Beispiel für die voneinander unterscheidbaren Objekte einen gelben Apfel und für die nicht voneinander unterscheidbaren Objekte nehmen wir zwei rote Äpfel. Wir haben damit 3 Äpfel und damit auch 3 Platzierungsmöglichkeiten. Für den ersten roten Apfel gibt es drei Platzierungsmöglichkeiten, nämlich alle. Für den zweiten gelben Apfel kommen nur noch 2 (3 – 1) Möglichkeiten in Betracht, da ja ein Platz durch den roten Apfel bereits belegt ist. Für den dritten Apfel ist es dagegen nur noch 1 (3 – 2) Möglichkeiten, da inzwischen durch die anderen beiden Äpfel zwei Plätze belegt sind.

Nun kannst du den ersten roten Apfel nicht gleich auf den ersten Platz legen, sondern auf den zweiten und den zweiten roten Apfel auf den ersten Platz. So kannst die Äpfel in eine beliebige Reihenfolge bringen. Die Anzahl der möglichen Platzierungen (Permutationen) von diesen 3 Objekten kannst du auch berechnen. Dazu benötigst du die Fakultät einer Zahl, in diesem Fall die der Zahl 3. Die Fakultät wird durch ein Ausrufezeichen dargestellt und steht hinter der Zahl, beispielsweise 3!. Bei der Fakultät werden alle ganzen Zahlen zwischen der angegebenen Zahl und der Zahl 1 miteinander multipliziert. In deinem Beispiel lautet die Fakultät 3! = 3 · 2 · 1 = 6. Du hast bei diesen 3 Äpfel also 6 verschiedene Platzierungsmöglichkeiten bzw. Permutationen:

Wie du jedoch sehen kannst, sind einige Reihen genau gleich, beispielsweise die erste und die dritte Reihe. Dies kommt daher, dass das Vertauschen der beiden roten Äpfel keine neue Reihenfolge bringt.

Daher verringert sich die Anzahl an Platzierungsmöglichkeiten bzw. Permutationen von ursprünglich 6 auf nur noch 3. Die Berechnung dazu erfolgt durch die Formel 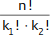. Der Zähler gibt an, wie viele Objekte du insgesamt hast, also n = 3 Äpfel → 3!. Der Nenner gibt an, wie viele verschiedene Objekte du hast. Wir haben 2 rote Äpfel, also k₁ = 2 → 2! und 1 gelben Apfel, also k₂ = 1 → 1!. Wenn du das in die Formel einsetzt, erhältst du als Ergebnis 3 Platzierungsmöglichkeiten bzw. Permutationen ().

Eine Permutation mit Wiederholung ist eine Anordnung von Objekten, von den nicht alle von einander unterscheidbar sind (einige Objekte sind gleich). Durch Vertauschen der gleichen Objekte ergibt sich keine neue Reihenfolge, was die Anzahl der maximale Platzierungsmöglichkeiten verringert.