Produktmenge

Wenn sich viele Menschen an einem Ort befinden, spricht man von einer Menschenmenge. Befindet sie viel Obst an einem Ort, spricht man von einer Obstmenge. Bei den Zahlen ist es nicht anders: Wenn sich viele Zahlen an einem Ort befinden, spricht man eben von einer Zahlenmenge. Du kannst mit zwei verschiedenen Obstmengen unterschiedliche Kombinationen darstellen.

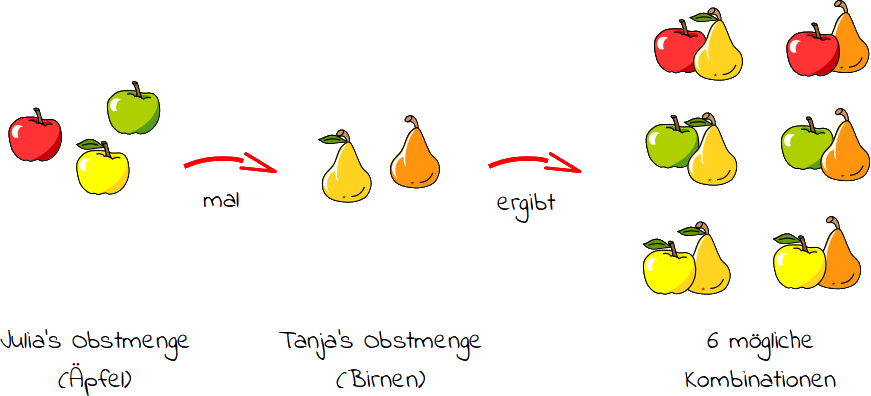
Wenn du dir jetzt Julia's Obstmenge anschaust, siehst du, dass sie drei Äpfel hat: einen roten, grünen und einen gelben Apfel. Tanja's Obstmenge hingehen besteht aus zwei Birnen: einer gelben und einer orangefarbenen Birne. Mit diesen 5 Früchten kannst du nun verschiedene Kombinationen legen. Zu jedem Apfel von Julia kannst du eine Birne von Tanja legen, also zwei Kombinationen pro Apfel. Bei den 3 Äpfel von Julia sind insgesamt 6 verschiedene Kombinationen möglich.

Mit den Zahlen ist es nicht anders: Die Produktmenge enthält alle Kombinationen aus der Multiplikation beider Mengen. Jedes Element der Menge M wird mit allen Elementen der Menge N multipliziert. Geschrieben wird das P = M x N.

P = M x N = {(a, b) | (a ∈ M) ∧ (b ∈ N)}

Den ersten Teil der oben stehenden „Hieroglyphen“ kennst du ja bereits: Die Produktmenge P ist die Menge M mal (x) die Menge N. In der geschweiften Klammer steht die genaue Bedingung für die Elemente, damit sie zur Produktmenge P gehören: das Element (a) muss ein Element der Menge M sein (a ∈ M), es muss also in der Menge M vorkommen. Das kleine Dach (∧) bedeutet »und«, also existiert noch eine Bedingung für die Zugehörigkeit zur Produktmenge. Und du kennst ja auch schon bereits: das Element (b) muss ein Element der Menge N sein (x ∈ N), es muss also in der Menge N vorkommen.

Der Begriff Differenzmenge wurde 1884 von Georg Cantor (1845-1918) eingeführt, der die Mengenlehre erfunden hat.

Die Menge M enthält die fünf Elemente 1, 2, 3, 4 und 5. Die Menge N enthält die drei Elemente 6, 7 und 8. Multiplizierst du nun jedes Element aus der Menge M mit jedem Element aus der Menge N, so ergeben sich 15 Kombinationen. Das erste Element aus M multipliziert mit jedem Element aus N ergibt die 3 Kombinationen 1 · 6, 1 · 7 und 1 · 8. Die weiteren Elemente ergeben folgende Kombinationen: 2 · 6, 2 · 7, 2 · 8, 3 · 6, 3 · 7, 3 · 8, 4 · 6, 4 · 7 ,4 · 8, 5 · 6, 5 · 7 und 5 · 8.

Die Produktmenge erhältst du, wenn du die Elemente aus der ersten Menge mit allen Elementen aus der zweiten Menge multiplizierst