Sierpinski-Teppich
Der Kreis hat von allen mathematischen Flächen die kleinsten Umfang bei größtem Flächeninhalt. Es gibt natürlich auch eine Fläche, die bei größtem Umfang den kleinsten Flächeninhalt hat. Diese Fläche nennt sich Sierpinski-Teppich. Er ist ein Fraktal, das ist ein Objekt, das aus mehreren verkleinerten Kopien seiner selbst besteht. Entdeckt bzw. erfunden hat ihn der polnische Mathematiker Wacław Sierpiński (1882 – 1969).
| So erhältst du den Sierpinski-Teppich: | So sieht's aus: |
|---|---|
|
1.
Die Ausgangsfläche des Sierpinski-Teppichs ist ein Quadrat (Stufe 0). |
Stufe 0 |
|
2.
In der 1. Stufe wird dieses Quadrat in 9 Teilquadrate zerlegt. |
Stufe 1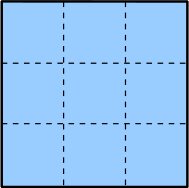 |
|
3.
Nun wird das mittlere Teilquadrat entfernt, 8 Teilquadrate bleiben übrig (9 – 1 = 8). |
Stufe 1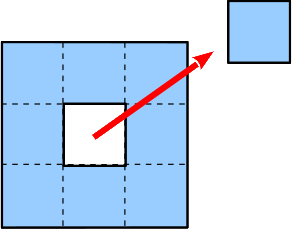 |
|
4.
Am Ende der 1. Stufe erhältst du nun ein „durchlöchertes“ Quadrat. Diese Fläche hat aufgrund des Loches ein kleineres Volumen, da an einem Loch kein Volumen vorhanden ist. Dieses Loch bewirken aber, dass der Umfang des Quadrats größer wird, da jeder Lochumfang zum Umfang hinzu gezählt wird. |
Stufe 1 |
|
5.
In der 2. Stufe baust du dir aus weiteren 7 solcher „Löcherquadrate“ wieder einen Löcherquadrat, das wieder das gleiche Aussehen hat. So erhältst du eine „sehr durchlöcherte“ Fläche, deren Flächeninhalt noch kleiner, aber deren Umfang riesengroß ist. |
Stufe 2 |
|
6.
In der 3. Stufe baust du dir aus weiteren 7 solcher „Löcherquadrate“ wieder einen Löcherquadrat, das auch wieder das gleiche Aussehen hat. So erhältst du eine „extrem durchlöcherte“ Fläche, deren Flächeninhalt nochmals kleiner, aber deren Umfang riesengroß ist. Je weiter du dieses Spielchen treibst, desto kleiner wird der Flächeninhalt, bis er irgendwann gegen Null geht und desto größer wird der Umfang, bis er irgendwann unendlich groß ist. |
Stufe 3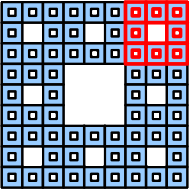 |
Der Sierpinski-Teppich ist eine Fläche, die bei kleinstem Flächeninhalt den größten Umfang hat. Er ist ein Fraktal, ein Objekt, das aus mehreren verkleinerten Kopien seiner selbst besteht.
Das könnte dich auch interessieren
Du hast einen Fehler gefunden oder möchtest uns eine Rückmeldung zu diesem Eintrag geben? Rückmeldung geben