Steigung
Fährst du gerne mit dem Fahrrad? Je nach dem, wo du fährst, ist der Radweg eben oder er steigt und fällt immer wieder an. Dieses auf und ab des Radweges wird Steigung genannt. Kleine Steigungen kannst du noch einfach bewältigen, bei großen Steigungen kommst du schnell außer Puste. So ein Radweg ist in der Mathematik wie eine Gerade oder Stecke. Daher können wir schon jetzt etwas über eine Gerade sagen: bei einer kleinen Steigung verläuft sie relativ flach, bei einer großen Steigung ist sie dagegen sehr steil.
Eine Steigung gibt den Höhenunterschied während eines bestimmten Längenunterschiedes an. Der Radweg steigt auf 500 m um 12 m an. Das bedeutet, während einer Länge von 500 m werden 12 m Höhe überwunden.

In der Mathematik hast du es vor allem bei linearen Funktionen mit der Steigung zu tun. Die allgemeine Funktionsgleichung einer linearen Funktion lautet y = mx + b. Dabei steht das m für die Steigung. Wenn du eine lineare Funktion zeichnest, erhältst du als Schaubild eine Gerade. Um die Steigung dieser Geraden zu berechnen, brauchst du zunächst zwei beliebige Punkte, die auf der Geraden liegen. Denn jetzt musst du den Höhenunterschied und den Längenunterschied der beiden Punkte berechnen: Für den Höhenunterschied subtrahierst du die y-Koordinaten der beiden Punkte und für den Längenunterschied subtrahierst du die x-Koordinaten der beiden Punkte. Anschließend dividierst du den Höhenunterschied durch den Längenunterschied, um die Steigung zu erhalten.
| So bestimmst du die Steigung: | So sieht's aus: |
|---|---|
| Eine lineare Funktion hat die Gleichung y = 0,5x + 1. Du sollst die Steigung berechnen bzw. überprüfen. | y=0,5x+1 |
|
1.
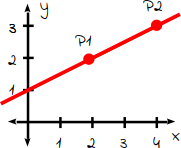
Das Schaubild wurde inzwischen gezeichnet. Suche dir auf der Geraden zwei beliebige Punkte heraus: Unsere heißen P1 und P2. |
 |
|
2.
Für den „Höhenunterschied“ (Δy) benötigst du die y-Koordinaten der beiden Punkte: P1 hat als y-Koordinate den Wert 2 und P2 hat den Wert 3. Subtrahiere nun die beiden Werte: 3 – 2 = 1. |
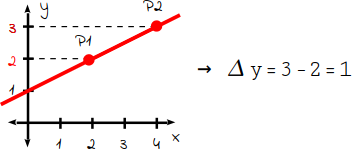 |
|
3.
Für den „Längenunterschied“ (Δx) benötigst du die x-Koordinaten der beiden Punkte: P1 hat als x-Koordinate den Wert 2 und P2 hat den Wert 4. Subtrahiere nun die beiden Werte: 4 – 2 = 2. |
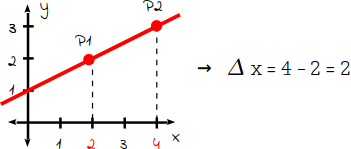 |
|
4.
Um die Steigung m zu berechnen, dividierst du den Höhenunterschied durch den Längenunterschied: 1 : 2 = 0,5. |
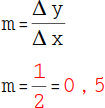 |
|
5.
Die Steigung beträgt 0,5. Dieser Wert steht auch in der Gleichung (vor dem x), du hast richtig gerechnet. |
m=0,5 → y=0,5x+1 |
Du hast im obigen Beispiel die Steigung mit 0,5 errechnet. Das bedeutet, dass pro x-Einheit die Gerade um 0,5 y-Einheiten ansteigt. Jedes Mal, wenn du um einen x-Wert weitergehst, steigt die Gerade um einen halben y-Wert. Sollte deine Steigung negativ sein, so fällt deine Gerade nach rechts ab. Das bedeutet, dass pro x-Einheit die Gerade um 0,5 y-Einheiten fällt.
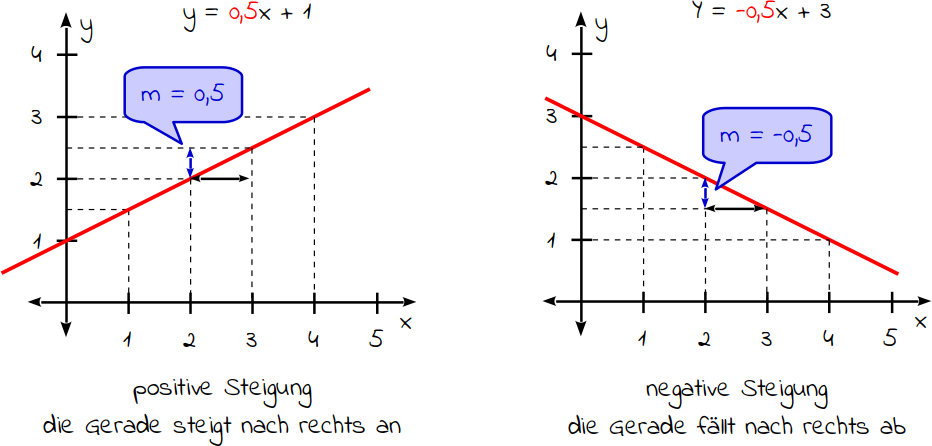
Die Steigung gibt an, wie stark eine Gerade ansteigt. Bei einer negativen Steigung fällt die Gerade ab. Je größer die Steigung, desto mehr y-Einheiten werden pro x-Einheit überwunden.
.
Das könnte dich auch interessieren
Du hast einen Fehler gefunden oder möchtest uns eine Rückmeldung zu diesem Eintrag geben? Rückmeldung geben