Verhältnisse in der Pyramide

Das Berechnen einer Pyramide beherrschten schon die Gelehrten im alten Ägypten von etwa 5.000 Jahren. Sie machten sich dabei die Verhältnisse zunutze, die in einer Pyramide vorliegen. Dabei werden die Pyramide und die entsprechenden Seiten aufgeschnitten und in rechtwinklige Teildreiecke zerlegt. Die Berechnung eines rechtwinkligen Dreiecks ist mit Hilfe der Winkelfunktionen oder dem Satz des Pythagoras möglich.

• Beim halben Diagonalschnitt (gelbe Fläche) wird die Pyramide entlang einer Diagonalen in der Mittel aufgeschnitten. Es entsteht dabei ein gleichschenkliges Dreieck, das wiederum in ein rechtwinkliges Dreieck halbiert wird. Ihre Seitenlinien entsprechen der Länge der Seitenkante der Pyramide (s), der Höhe der Pyramide (h) und der Hälfte der Länge der Diagonalen ().
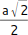• Beim halben Parallelschnitt (blaue Fläche) wird die Pyramide parallel zu der Grundkante in der Mittel aufgeschnitten. Es entsteht dabei ein gleichschenkliges Dreieck, das wiederum in ein rechtwinkliges Dreieck halbiert wird. Ihre Seitenlinien entsprechen der Höhe der Pyramide (h), der Höhe der Seitenfläche (h_s) und der Hälfte der Länge der Grundfläche ().
• Bei der halben Seitenfläche (grüne Fläche) wird eine Seitenfläche der Pyramide entlang ihrer Mittellinie abgeschnitten. Es entsteht dabei ein rechtwinkliges Dreieck. Ihre Seitenlinien entsprechen der Höhe der Seitenfläche (h_s), der Länge der Seitenkante der Pyramide (s) und der Hälfte der Länge der Grundfläche ().

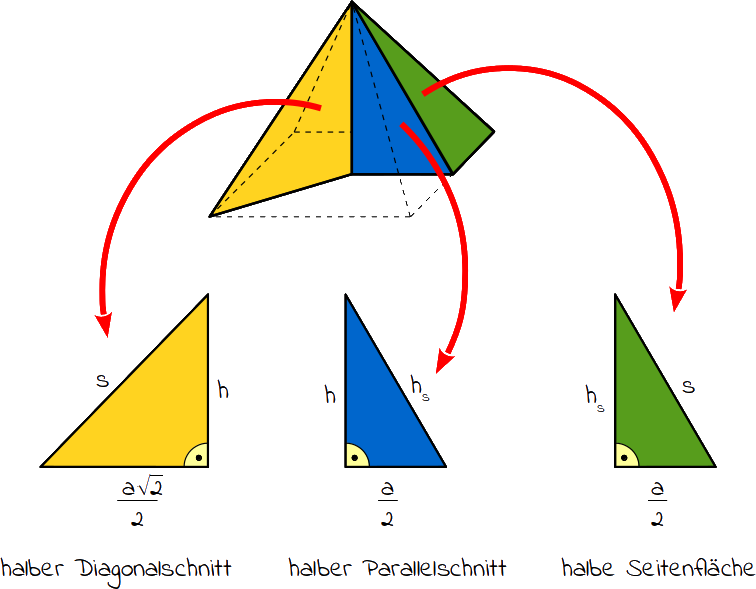
Wenn du eine Pyramide in verschiedene Teildreiecke zerlegst, fällt dir die Berechnung leichter.

Mein Tipp: In unserer Bastelecke findest du einen Bastelbogen, mit dem du dir ein tolles Modell dieser aufgeschnittenen Pyramide basteln kannst.