Konstruktion eines Höhenschnittpunktes
Eine Höhe ist ein Element der Geometrie und stellt dabei vereinfacht eine gerade Linie dar. Sie ist eine geradlinige (nicht gekrümmte) und dünne Linie, die senkrecht auf einer Seite steht.
Der größte rechtwinklige Abstand einer Seite zum gegenüberliegenden Eckpunkt in einer Fläche wird Höhe genannt. Eine Höhe steht also immer im rechten Winkel (90°) auf einer Seite und endet in dem Eckpunkt, der dieser Seite gegenüber liegt. Wenn du alle 3 Höhen in einem Dreieck einzeichnest, dann siehst du, dass sie sich alle in einem gemeinsamen Punkt schneiden. Dieser Punkt wird Höhenschnittpunkt genannt.
Du sollst den Höhenschnittpunkt eines stumpfwinkligen Dreieck (ein Winkel ist größer als 90°) konstruieren, die auf der Seite c steht. Zum Konstruieren einer Höhe benötigst du deinen Bleistift und dein Geodreieck. Da bei diesem Dreieck die Eckpunkte A und C nicht mehr oberhalb der Seiten liegen, musst du eine Verlängerungslinie zeichnen. Drehe anschließend dein Geodreieck so, bis die Seite c durch die 90°-Markierung geht. Das ist meistens der lange Strich in der Mitte deines Geodreiecks. Nun verschiebst du es so lange, bis die Kante des Geodreiecks durch den gegenüberliegenden Eckpunkt geht. Zeichne dann die Höhen entlang dem Geodreieck ein. An dem Punkt, an dem sich alle Höhen schneiden, liegt der Höhenschnittpunk.
| So konstruierst du einen Höhenschnittpunkt: | So sieht's aus: |
|---|---|
|
1.
In diesem stumpfwinkligen Dreieck sollst du den Höhenschnittpunkt einzeichnen (die Vorgehensweise ist bei spitzwinkligen Dreiecken ähnlich). |
 |
|
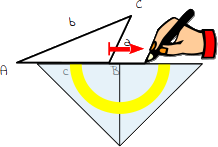
2.
Bei diesem Dreieck liegt der Eckpunkt C nicht mehr oberhalb der Seite c, sondern außerhalb. Verlängere daher die Seite c, indem du dein Geodreieck an die Seite c anlegst und eine Verlängerungslinie nach rechts zeichnest. |
 |
|
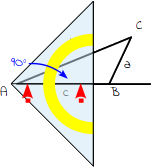
3.
Drehe dein Geodreieck so, dass die Seite c durch die 90°-Markierung geht (das ist meistens der lange Strich in der Mitte deines Geodreiecks). Auf diese Weise kannst du sehr schnell und einfach rechte Winkel einzeichnen. |
 |
|
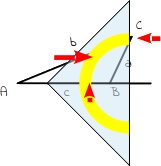
4.
Nun verschiebst du das Geodreieck so lange, bis die Kante des Geodreiecks durch den gegenüberliegenden Eckpunkt C geht. Du musst es hierbei auf die eben gezeichnete Verlängerungslinie weiterschieben. Achte beim Verschieben darauf, dass die 90°-Markierung nicht verrutscht. |
 |
|
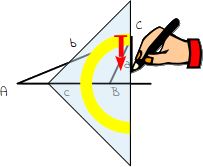
5.
Zeichne nun die Höhe der Seite c entlang dem Geodreieck ein. |
 |
|
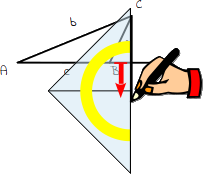
6.
Verschiebe dein Geodreieck ein wenig nach unten und verlängere die Höhe der Seite c um ein gutes Stück. |
 |
|
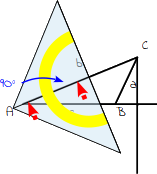
7.
Drehe dein Geodreieck so, dass die Seite b durch die 90°-Markierung geht. |
 |
|
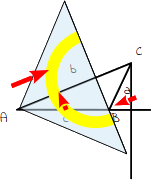
8.
Nun verschiebst du das Geodreieck so lange, bis die Kante des Geodreiecks durch den gegenüberliegenden Eckpunkt B geht. Achte beim Verschieben darauf, dass die 90°-Markierung nicht verrutscht. |
 |
|
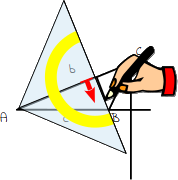
9.
Zeichne nun die Höhe der Seite b entlang dem Geodreieck ein. |
 |
|
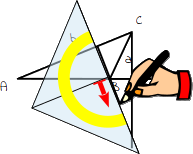
10.
Verschiebe dein Geodreieck ein Stück nach unten und verlängere auch die Höhe der Seite b, bis sie die Höhe der Seite c schneidet. |
 |
|
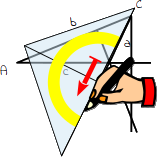
11.
Auch der Eckpunkt A liegt nicht mehr oberhalb der Seite a, sondern außerhalb. Verlängere daher ebenso die Seite a, indem du dein Geodreieck an die Seite a anlegst und eine Verlängerungslinie nach unten zeichnest. |
 |
|
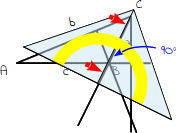
12.
Drehe dein Geodreieck so, dass die Seite a durch die 90°-Markierung geht. |
 |
|
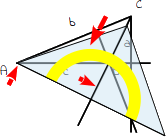
13.
Nun verschiebst du das Geodreieck so lange, bis die Kante des Geodreiecks durch den gegenüberliegenden Eckpunkt A geht. Du musst es hierbei auf die eben gezeichnete Verlängerungslinie weiterschieben. Achte beim Verschieben darauf, dass die 90°-Markierung nicht verrutscht. |
 |
|
14.
Zeichne nun die Höhe der Seite a entlang dem Geodreieck ein. |
 |
|
15.
Dieses Mal kannst du dein Geodreieck liegen lassen. Verlängere die Höhe der Seite a, bis sie durch den Schnittpunkt der beiden anderen Höhen geht. |
 |
|
16.
Fertig - du hast nun einen Höhenschnittpunkt konstruiert, in dem sich alle drei Höhen der Dreiecksseiten schneiden. Da es sich um ein stumpfwinkeliges Dreieck handelt, liegt er außerhalb des Dreiecks (bei einem spitzwinkeligen Dreieck würde er im Inneren liegen). |
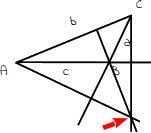 |
Alle Höhen in einem Dreieck schneiden sich in einem gemeinsamen Punkt, dem Höhenschnittpunkt.
Das könnte dich auch interessieren
Du hast einen Fehler gefunden oder möchtest uns eine Rückmeldung zu diesem Eintrag geben? Rückmeldung geben