Abschlussprüfung Mathematik für Realschule (2)

Fach Mathematik – Pflichtbereich

Zugelassene Hilfsmittel: Formelsammlung, elektronischer, nicht programmierbarer Taschenrechner sowie Parabelschablone und Zeichengeräte.

Hinweis:

Im Pflichtbereich musst du alle Aufgaben bearbeiten. Hier kannst du maximal 17 Punkte erreichen.

Pflichtbereich Aufgabe 1 (2 Punkte):

Berechne die Oberfläche einer quadratischen Pyramide mit a = 4,8 cm und s = 5,2 cm.

Pflichtbereich Aufgabe 2 (2 Punkte):

Ein Kegel ist gegeben durch die Höhe h = 3 cm und den Radius r = 4 cm.

Berechne die Mantelfläche und Volumen des Kegels.

Pflichtbereich Aufgabe 3 (2 Punkte):

Eine verschobene Normalparabel enthält die Punkte P (– 6|5) und Q (0|– 5).

Bestimme ihre Gleichung.

Pflichtbereich Aufgabe 4 (2,5 Punkte):

Eine nach oben geöffnete Parabel besitzt den Scheitel S (– 3,5|– 1,5).

Überprüfe rechnerisch, ob die Punkte P (– 4,5|6) und Q (0,5|14,5) auf der Parabel liegen.

Pflichtbereich Aufgabe 5 (2,5 Punkte):

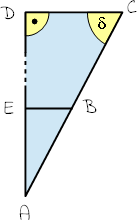
Die Entfernung der Punkte A und D kann aufgrund eines Hindernisses nicht direkt gemessen werden. Folgende Größen sind gegeben:

BC = 1.356 cm

BE = 352 cm

δ = 65,0°

Berechne die Länge AD.

Pflichtbereich Aufgabe 6 (2 Punkte):

Löse das Gleichungssystem:

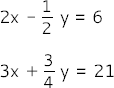
Pflichtbereich Aufgabe 7 (2 Punkte):

Bestimme die Lösungsmenge.

x² – 15x + 36 = 0

Pflichtbereich Aufgabe 8 (2 Punkte):

Julia legt bei ihrer Bank am Anfang des Jahres einen bestimmten Betrag an. Der Zinssatz beträgt 3,75 %.

Nach einem Jahr hebt sie 5.500 € ab. Nach Ablauf eines weiteren Jahres beträgt ihr Kapital 37.350,00 €. Die Zinsen werden mit verzinst.

a) Welchen Betrag hat sie angelegt?

b) Wie viel Zinsen wurden ihr in den beiden Jahren insgesamt gutgeschrieben?

Fach Mathematik – Wahlbereich

Zugelassene Hilfsmittel: Formelsammlung, elektronischer, nicht programmierbarer Taschenrechner sowie Parabelschablone und Zeichengeräte.

Hinweis:

Im Wahlbereich musst du zwei von drei Aufgaben bearbeiten. Hier kannst du maximal 16 Punkte erreichen.

Wahlbereich Aufgabe 1 (4,5 Punkte + 3,5 Punkte):

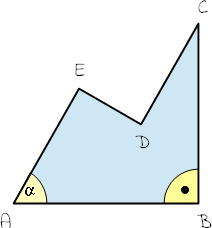
1. Von der Figur ABCDE sind gegeben:
   
   BC = 9,3 cm
   
   DE = 4,1 cm
   
   AE = 8,6 cm
   
   α = 50°
   
   Berechne den Flächeninhalt der Figur.
   
   
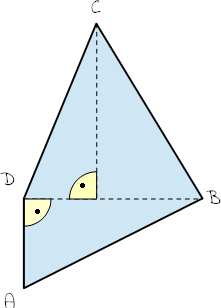
2. Gegeben ist das Viereck ABCD. Es gilt:
   
   AD = 12,4 cm
   
   A_ABD = 138,9 cm²
   
   BC = 30,4 cm
   
   Winkel CBD = 60,8°
   
   Berechne den Winkel BDC.
   
   

Wahlbereich Aufgabe 2 (5 Punkte + 3 Punkte):

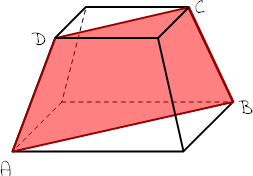
1. Der Diagonalschnitt eines quadratischen Pyramidenstumpfs hat die Maße:
   
   A_ABCD = 55,0 cm²
   
   AB = 9,8 cm
   
   CD = 4,8 cm
   
   1. Berechne die Mantelfläche des Pyramidenstumpfs.
   
   2. Welche Höhe hat die Ergänzungspyramide?
   
   
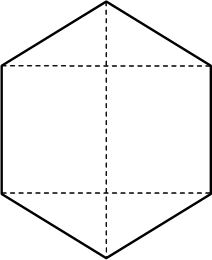
2. Ein Zylinder mit zwei aufgesetzten Kegeln hat als Achsenschnitt ein regelmäßiges Sechseck mit dem Flächeninhalt
   
   .
   
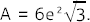   Berechne die Oberfläche des zusammengesetzten Körpers in Abhängigkeit von e ohne Verwendung gerundeter Werte.
   
   

Wahlbereich Aufgabe 3 (3 Punkte + 5 Punkte):

1. Eine Parabel p₁ hat die Gleichung y = x² + px + 6 und geht durch den Punkt P (3|6).
   
   Eine Parabel p₂ hat die Gleichung y = – 2x² + c und geht durch den Punkt Q (2|– 2).
   
   Berechne die Koordinaten der Schnittpunkte der beiden Parabeln.
2. Eine nach oben geöffnete verschobene Normalparabel wird von der Geraden g in den Punkten P₁ (1|3) und P₂ (6|8) geschnitten.
   
   Eine zur Geraden g parallele Gerade h geht durch den Punkt B (3,5|– 0,75).
   
   Weise rechnerisch nach, dass B der einzige gemeinsame Punkt der Parabel und der Geraden h ist.