Abschlussprüfung Mathematik für Realschule (3)

Fach Mathematik – Pflichtbereich

Zugelassene Hilfsmittel: Formelsammlung, elektronischer, nicht programmierbarer Taschenrechner sowie Parabelschablone und Zeichengeräte.

Hinweis:

Im Pflichtbereich musst du alle Aufgaben bearbeiten. Hier kannst du maximal 17 Punkte erreichen.

Pflichtbereich Aufgabe 1 (2 Punkte):

Eine nach oben geöffnete Normalparabel hat den Scheitelpunkt S (– 0,5|– 4).

Berechne die Koordinaten der Schnittpunkte der Parabel mit der x-Achse bzw. der y-Achse./p>

Pflichtbereich Aufgabe 2 (2 Punkte):

Löse das Gleichungssystem:

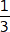x – 2y = – 1

2x – y = 4x – 7

Pflichtbereich Aufgabe 3 (2,5 Punkte):

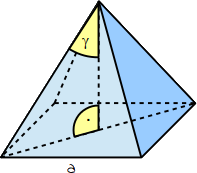
Eine quadratische Pyramide hat die Maße a = 6,8 cm und γ = 37,0°.

Berechne die Oberfläche der Pyramide.

Pflichtbereich Aufgabe 4 (2 Punkte):

Eine Kugel hat das Volumen V = 589 cm³. Ihr Radius ist gleich groß wie der Grundkreisradius eines volumengleichen Kegels.

Berechne die Mantelfläche des Kegels.

Pflichtbereich Aufgabe 5 (2 Punkte):

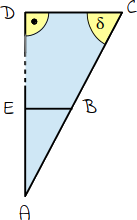
Die Entfernung der Punkte A und D kann aufgrund eines Hindernisses nicht direkt gemessen werden. Folgende Größen sind gegeben:

BC = 1.356 cm

BE = 352 cm

δ = 65,0°

Berechne die Länge AD.

Pflichtbereich Aufgabe 6 (2,5 Punkte):

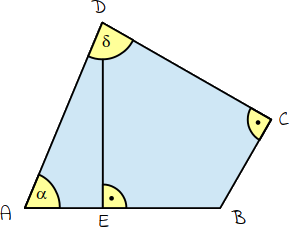
Vom Viereck ABCD sind bekannt:

BC = 4,0 cm

CD = 6,3 cm

α = 54,0°

γ = 110°

Berechne die Länge DE.

Pflichtbereich Aufgabe 7 (1,5 Punkte):

Bei einer Qualitätskontrolle wurde bei 24 % aller überprüften Smartphones ein Mangel festgestellt. 18 % dieser Mängel waren nicht mehr zu reparieren; das waren 27 Smartphones.

Wie viele Smartphones wurden überprüft?

Pflichtbereich Aufgabe 8 (2 Punkte):

Ein Kapital von 28.000 € wird 5 Jahre lang angelegt, Zinsen werden mitverzinst.

Zinssatz im 1. Jahr: 2,0 %

Zinssatz im 2. Jahr: 2,5 %

Zinssatz im 3. Jahr: 3,5 %

Zinssatz im 4. Jahr: 5,0 %

Für das fünfte Jahr werden 2.067,88 € Zinsen gutgeschrieben.

a) Wie hoch ist der Zinssatz im fünften Jahr?

b) Bei welchem jährlich gleichbleibenden Zinssatz hätte sich nach fünf Jahren das gleiche Endkapital ergeben?

Fach Mathematik – Wahlbereich

Zugelassene Hilfsmittel: Formelsammlung, elektronischer, nicht programmierbarer Taschenrechner sowie Parabelschablone und Zeichengeräte.

Hinweis:

Im Wahlbereich musst du zwei von drei Aufgaben bearbeiten. Hier kannst du maximal 16 Punkte erreichen.

Wahlbereich Aufgabe 1 (4 Punkte + 4 Punkte):

1. Von der regelmäßigen achtseitigen Pyramide sind bekannt:
   
   Grundkante a = 6,4 cm
   
   Körperhöhe h = 15,1 cm
   
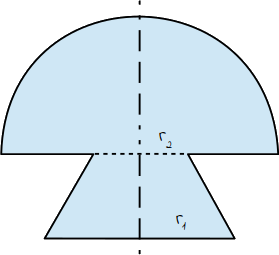
   Berechne die Oberfläche der Pyramide.
2. Ein zusammengesetzter Körper besteht aus einem Kegelstumpf und einer Halbkugel. Es gilt:
   
   r₁ = 7e
   
   r₂ = 4e
   
   V_Kegelstumpf = 124πe³
   
   V_Halbkugel = 486πe³
   
   Zeige ohne Verwendung gerundeter Werte, dass sich die Oberfläche des Körpers mit der Formel O = 331πe² berechnen lässt.
   
   

Wahlbereich Aufgabe 2 (5 Punkte + 3 Punkte):

1. Vom Viereck ABDE sind bekannt:
   
   AB = 4,9 cm
   
   AE = 6,2 cm
   
   BD = 7,8 cm
   
   Winkel DBA = 73°
   
   1. Berechne den Abstand des Punktes D von AB.
   
   2. Wie groß ist der Winkel ε?
   
   Der Flächeninhalt des Dreiecks BCD ist halb so groß wie der Flächeninhalt des Vierecks ABDE.
   
   3. Wie groß ist der Winkel DCB?
   
   
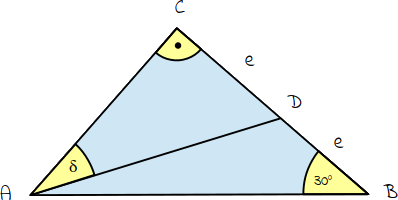
2. Zeige ohne Verwendung gerundeter Werte, dass im nebenstehenden Dreieck ABC gilt:
   
   
   
   

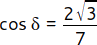
Wahlbereich Aufgabe 3 (4 Punkte + 4 Punkte):

1. Eine Parabel p₁ mit der Gleichung y = x² + 2x + q geht durch den Punkt P (- 3|- 1).
   
   Eine zweite Parabel p₁ hat die Gleichung y = - x².
   
   1. Zeichne beide Parabeln in ein Koordinatensystem ein.
   
   2. Berechne die Punkte der Koordinaten der Schnittpunkte der beiden Parabeln.
   
   3. Bestimme rechnerisch die Gleichung der Geraden, die durch diese beiden Schnittpunkte verläuft.
2. Bestimmte die Definitionsmenge und die Lösungsmenge der Gleichung: