duale Körper

Ein dualer Körper ist ein Begriff aus der Geometrie. Das Wort dual stammt von dem lateinisch Wort dualis, das »zwei enthaltend« bedeutet. Ein dualer Körper ist also ein Körper bzw. Polyeder, der noch einen zweiten Körper enthält. Diesen „zweiten“ (dualen) Körper kannst du ganz leicht herausfinden: Dazu markierst du dir die Mittelpunkte aller Seitenflächen des Polyeders. Diese Mittelpunkte stellen nun die Eckpunkte eines neuen Körpers dar. Verbindest du diese, erhältst du wieder einen Körper. Sozusagen ein Körper-im-Körper. Und schon hast du den dualen Körper gefunden. Dieser neue Körper hat zwangsweise genauso viele Ecken wie der Ursprungskörper an Flächen hat, auch die Kantenanzahl ist gleich.

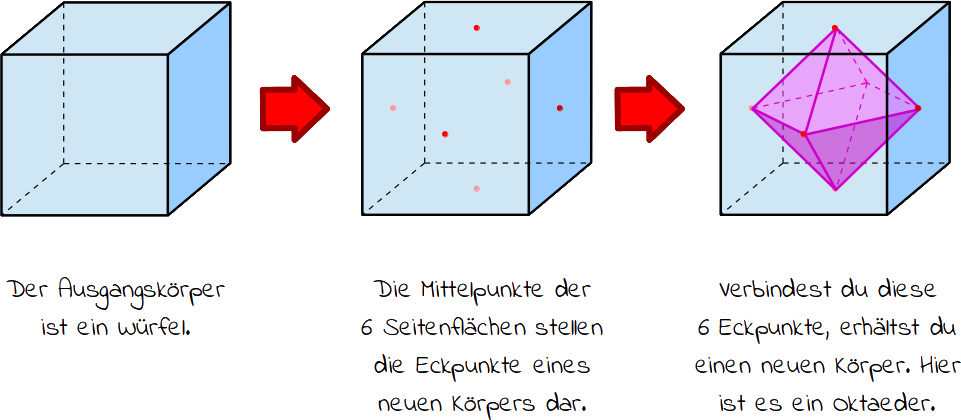
Nehmen wir als Beispiel einen Würfel. Er besteht aus 6 gleich großen Quadraten als Seitenflächen. Diese 6 Seitenflächen bilden zusammen 8 Ecken und 12 Kanten. Die Mittelpunkte der 6 Quadrate werden nun zu Eckpunkte eines neuen Körpers. Wenn du diese 6 Eckpunkte verbindest, erhältst du einen neuen Körper, der ebenfalls 12 Kanten hat. Dieser Körper nennt man Oktaeder (da er 8 Seitenflächen hat). Daher stellt das Oktaeder der duale Körper des Würfels dar.

Wenn du umgekehrt die Mittelpunkte der Seitenflächen des Oktaeders verbinden würdest, hättest du wieder einen Würfel.

Verbindest du die Mittelpunkte der Seitenlinien eines Körpers miteinander, so erhältst du einen neuen Körper. Dieser neue Körper hat so viele Ecken, wie der Ursprungs-körper an Seiten hat, auch die Kantenanzahl ist gleich. Solche Körper werden duale Körper genannt.