Formeln umstellen

Das Wort Formel stammt vom lateinischen »formula«, das übersetzt »Form« bedeutet. Es steht daher für eine bestimmte Form oder Folge von Buchstaben, Zahlen, Zeichen, Symbolen oder Worten zur verkürzten Bezeichnung eines Sachverhalts. Formeln stellt einen Zusammenhang zwischen mathematischen Größen dar.

Hier einmal ein Beispiel für eine Formel. Diese Formel u = 2 · (a + b) dient der Berechnung des Umfangs eines Rechtecks. Sie enthält zwei variable Elemente a und b, die jeweils für die Länge (a) und die Breite (b) des Rechteckes stehen. Kennst du diese Werte, so kannst du den Umfang u über das Verhältnis berechnen. Hin und wieder begegnen dir jedoch Aufgaben, zu denen zwar eine Formel passt, du diese jedoch nicht anwenden kannst, weil beispielsweise der Endwert bereits gegeben ist. In diesem Fall musst du die Formel umstellen. Bei diesem Rechteck ist der Umfang mit 14 cm und die Länge mit 4 cm bereits gegeben. Gesucht ist die Breite des Rechtecks. Um diese Breite nun zu berechnen, musst du die Formel für den Umfang nach der Breite b umstellen.

Wenn du eine Formel umstellen musst, dann muss der gesuchte Wert alleine auf einer Seite des Gleichheitszeichens stehen. Schaue dir dazu die einzelnen Elemente der Rechnung an und wie sie miteinander verknüpft sind. Bei der Umfangsformel ist die die 2 und die Klammer, verknüpft mit einem Malpunkt (Multiplikation). Zuerst kommt diese 2 auf die andere Seite. Da sie durch eine Multiplikation verknüpft, musst du die Gegenoperation anwenden. Bei einer Multiplikation ist das die Division, daher musst du durch 2 dividieren. Anschließend kommt die 4 cm auf die andere Seite. Sie ist mit einem Pluszeichen (Addition) mit dem b verknüpft. Die Gegenoperation einer Addition ist die Subtraktion, daher musst du 4 cm subtrahieren. Das b steht nun alleine und du kannst es berechnen. Berechne zuerst den Bruch (14 cm · 2 = 7 cm) und anschließend die Subtraktion (7 cm - 4 cm = 3 cm). Die gesuchte Breite b des Rechtecks beträgt 3 cm.

So stellst du deine Formel um:	So sieht es aus:
Du hast die Formel für den Umfang eines Rechtecks. Sie besteht aus den beiden variablen Elementen a und b.	u=2·(a+b)
1. Gegeben sind der Umfang des Rechtecks u = 14 cm und die Länge des Rechtecks a = 4 cm. Ersetze daher in der Formel u = 2 · (a + b) diese Werte.	u=14cm a=4cm u=2·(a+b) → 14cm=2·(4cm+b)
2. Der Wert b für die Breite ist noch nicht bekannt. Diesen musst du nun berechnen. Dazu musst du die Formel nach b umstellen.	14cm=2·(4cm+b) b=?
3. Um die Formel nach b umzustellen, muss es alleine stehen. Zuerst kommt die 2 auf die andere Seite. Sie ist mit einem Malpunkt (Multiplikation) verknüpft, daher musst du durch 2 dividieren.
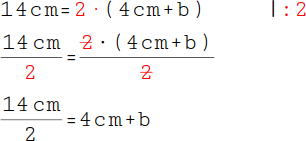4. Anschließend kommt die 4 cm auf die andere Seite. Sie ist mit einem Pluszeichen (Addition) verknüpft, daher musst du 4 cm subtrahieren.
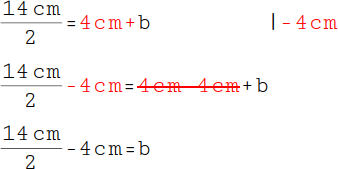5. Das b steht nun alleine und du kannst es berechnen. Berechne zuerst den Bruch: 14 cm · 2 = 7 cm
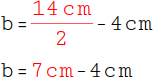6. Berechne zum Schluss die Subtraktion: 7 cm - 4 cm = 3 cm.	b=7cm-4cm b=3cm
7. Die Breite b des Rechtecks beträgt 3 cm.	b=3cm

Wenn du eine Formel umstellen musst, muss der gesuchte Wert alleine auf einer Seite des Gleichheitszeichens stehen. Die anderen Werte bekommst du mit der jeweiligen Gegenoperation (Addition ↔ Subtraktion, bzw. Multiplikation ↔ Division) auf die andere Seite. Anschließend kannst du den gesuchten Wert berechnen.