gleichschenkliges Trapez

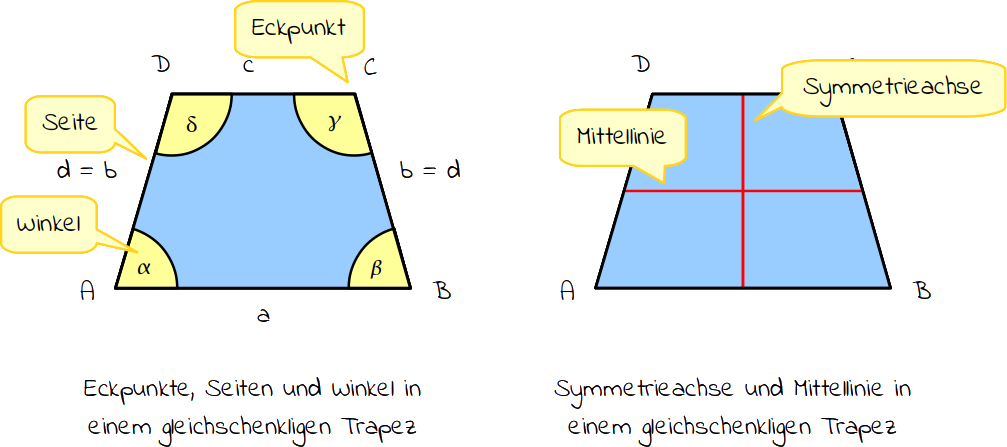
Ein gleichschenkliges Trapez (von altgriechisch trapeza „Tisch, Vierfuß“) ist eine geometrische Fläche mit 4 Ecken. Dazwischen liegen 4 Seiten, von denen zwei gleich lang sind (b = d). Die anderen beiden Seiten (a und c) sind parallel. Sie sind mit den Kleinbuchstaben a, b, c und d benannt. Dort, wo zwei Seiten aufeinander treffen, befindet sich ein Eckpunkt. Die Eckpunkte in einem Trapez werden oftmals mit A, B C und D bezeichnet. In jedem Eckpunkt befindet sich jeweils ein Winkel, die alle nicht rechtwinklig sind. Wenn du alle Winkel zusammenzählst (addierst) erhältst du 360° (Winkelsumme). Die beiden Winkel an einer der parallelen Seiten sind gleich groß (α = β bzw. γ = δ) . Die Winkel sind immer nach dem Eckpunkt benannt, in dem er liegt, d.h. der Winkel α (Alpha) liegt im Punkt A. Die anderen Winkel werden mit β (Beta), γ (Gamma) und δ (Delta) bezeichnet. Das gleichschenkliche Trapez hat 1 Symmetrieachse. Genau zwischen den parallelen Seitenlinien (a und c) befindet sich die Mittellinie m.

Formeln

Flächeninhalt
Umfang	u = a + 2b + c
Mittellinie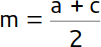
Winkelsumme	α + β + γ + δ = 360°

Ein gleichschenkliges Trapez ist eine Fläche mit vier Seiten, von denen zwei gleich lang sind. Die anderen beiden Seiten sind parallel. Zwei benachbarte Winkel sind gleich groß.