Kongruenzsatz 3

Wenn du zwei Dreiecke auf Form und Fläche vergleichen sollst, ist es am einfachsten, du legst die beiden Dreiecke aufeinander. Wenn dann nichts übersteht und sie exakt aufeinander passen, so sind sie in Form und Fläche gleich. Nun kannst du aber nicht immer die Dreiecke aufeinander legen, da du dein Mathebuch oder Matheheft nicht zerschneiden kannst. Du benötigst eine andere Methode, um die Gleichheit von Form und Fläche zu überprüfen. Daher wurden die sogenannten Kongruenzsätze erfunden. Das Wort Kongruenz stammt von dem lateinischen Wort »congruens« ab, das übereinstimmend bedeutet. Zwei Dreiecke sind kongruent (deckungsgleich), wenn sie in 3 Angaben übereinstimmen. Die einzelnen Kongruenzsätze legen dabei fest, welche 3 Angaben übereinstimmen müssen, damit Dreiecke als gleich in Form und Fläche angesehen werden können.

Der 3. Kongruenzsatz lautet:

Zwei Dreiecke sind kongruent, wenn sie in einer Seite und in den zwei anliegenden Winkel übereinstimmen.

Das bedeutet, zwei Dreiecke sind gleich in Form und Fläche (kongruent), wenn eine Seite genau gleich lang ist und die zwei Winkel, die an dieser Seite anliegen, gleich groß sind. Wenn du zwei Dreiecke hast, bei denen eine Seite und die beiden anliegenden Winkel des ersten Dreieckes (Δ_ABC) genau so groß sind, wie die gleiche Seite und die gleichen Winkel des zweiten Dreiecks (Δ_A'B'C'), so sind ihre Form und Fläche gleich. Wenn beispielsweise die Seite c in beiden Dreiecken genau gleich lang ist (c = c'), der links anliegende Winkel α in beiden Dreiecken genau gleich groß ist (α= α') und auch noch der rechts anliegende Winkel in beiden Dreiecken gleich groß ist (β = β'), dann können die Dreiecke als gleich in Form und Fläche (kongruent) angesehen werden. Legst du die beiden Dreiecke aufeinander, dann steht nichts über und sie passen exakt aufeinander. Abgekürzt wird der zweite Kongruenzsatz mit WSW, wobei das W für Winkel und S für Seite steht, also Winkel, Seite, Winkel.

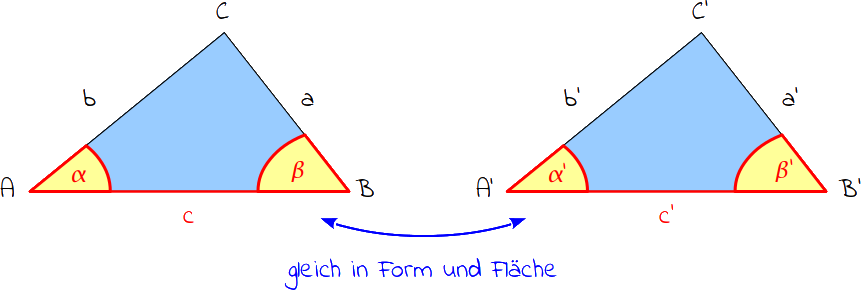
Der dritte Kongruenzsatz besagt, dass zwei Dreiecke gleich in Form und Fläche (kongruent) sind, wenn sie in einer Seite und den beiden anliegenden Winkel übereinstimmen (WSW).