Kreisdiagramm zeichnen
Ein Kreisdiagramm ist ein besonderes Diagramm, das die Werte im Verhältnis zueinander als Kreis darstellt. Du hast hierbei keine Achsen, wie bei einem gewöhnlichen Diagramm. Die Gesamtsumme aller Werte entspricht dem vollen Kreis. Die einzelnen Werte werden hierbei prozentual als Sektoren (Teilfläche) des gesamten Kreises dargestellt. Aus einem Diagramm können so recht schnell die einzelnen Werte abgelesen werden.
Eine Kinobesitzerin hat sich die Besucherzahlen der Monate Januar bis Mai notiert und möchte diese nun als Kreisdiagramm darstellen.
Um ein Kreisdiagramm zu erstellen, benötigst du zuerst einen Kreis: Lege dazu den Mittelpunkt des Kreisdiagramms fest, stelle den Zirkel auf einen Radius (z. B. 3 cm) ein und zeichne einen kompletten Kreisbogen. Zeichne noch eine gerade senkrechte Linie von der Kreisaußenlinie bis zum Mittelpunkt.
Jetzt geht es erst einmal ans Rechnen: Addiere alle Werte, in diesem Fall die Besucherzahlen, um die Gesamtsumme zu erhalten: 3.400 + 4.300 + 3.800 + 2.800 + 3.200 = 17.500. Die Gesamtsumme von 17.500 Besuchern stellen 100 % dar, das entspricht dem kompletten Kreis. Berechne für den ersten Wert (Januar) den prozentualen Anteil. Dividiere dazu den ersten Wert (3.400) durch die Gesamtsumme: 3.400 : 17.500 = 0,1943. Um für die spätere Beschriftung die Prozentzahl zu erhalten, multipliziere den Quotient mit 100: 0,1943 · 100 = 19 %. Mit dieser Prozentzahl kannst du jedoch nichts in dem Kreisdiagramm anfangen. Damit du dort Linien einzeichnen kannst, benötigst du eine Gradzahl. Da der komplette Kreis 360° sind, multipliziere den prozentualen Wert mit 360: 0,1943 · 360 = 70°. Der erste Sektor (Teilfläche) des Kreisdiagramms hat somit eine Winkelweite von 70°.
Lege das Geodreieck mit der langen Kante an die zuletzt gezeichnete senkrechte Linie. Verschiebe das Geodreieck soweit, bis die Nullmarkierung am Kreismittelpunkt liegt. Drehe das Geodreieck soweit nach unten, bis die 70°-Markierung der äußeren Skala durch die Linie geht. Achte beim Drehen darauf, dass sich die Nullmarkierung nicht verschiebt. Zeichne eine gerade Linie entlang dem Geodreieck vom Kreismittelpunkt bis zur Kreisaußenlinie. Lass das Geodreieck nach dem Zeichnen so liegen. Die von beiden Linien eingeschlossene Fläche entspricht dem ersten Wert (Januar).
Berechne für den zweiten Wert (Februar) die Winkelweite: Dividiere dazu den zweiten Wert (4.300) durch die Gesamtsumme und multipliziere den Quotient mit 360: 4.300 : 17.500 = 0,2457 · 360 = 88°. Multipliziere für die spätere Beschriftung den Quotient mit 100: 0,2457 · 100 = 25 %.
Der zweite Sektor des Kreisdiagramms hat eine Winkelweite von 88°. Drehe das Geodreieck weiter nach oben, bis die 88°-Markierung der äußeren Skala durch die Linie geht. Achte wieder beim Drehen darauf, dass sich die Nullmarkierung nicht verschiebt. Zeichne eine gerade Linie entlang dem Geodreieck vom Kreismittelpunkt bis zur Kreisaußenlinie.
Verfahre mit allen anderen Werten genauso, bis du alle Sektoren eingezeichnet hast. Beschrifte zum Schluss die einzelnen Sektoren mit dem Monatsnamen und der von dir berechneten Prozentzahl und male sie bunt aus.

| So erstellst du ein Kreisdiagramm: | So sieht's aus: |
|---|---|
| Diese Werte sollen in einem Kreisdiagramm dargestellt werden. | Januar: 3400 Februar: 4300 März: 3800 April: 2800 Mai: 3200 |
|
1.
Lege den Mittelpunkt des Kreisdiagramms fest, indem du mit deinem Bleistift einen Punkt zeichnest. |
 |
|
2.
Stelle den Zirkel auf einen Radius (z. B. 3 cm) ein. Steche die Spitze des Zirkels in den Mittelpunkt ein und zeichne einen kompletten Kreisbogen um den Mittelpunkt. |
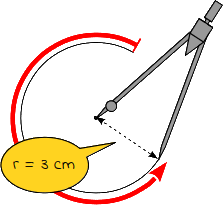 |
|
3.
Zeichne eine gerade senkrechte Linie von der Kreisaußenlinie bis zum Mittelpunkt. |
 |
|
4.
Addiere alle Werte, in diesem Fall die Besucherzahlen, um die Gesamtsumme zu erhalten: 3.400 + 4.300 + 3.800 + 2.800 + 3.200 = 17.500. |
3400+4300+3800+2800+3200 =17500 |
|
5.
Die Gesamtsumme von 17.500 Besuchern stellen 100 % dar. Berechne für den ersten Wert (Januar) den prozentualen Anteil. Dividiere dazu den ersten Wert (3.400) durch die Gesamtsumme: 3.400 : 17.500 = 0,1943. Um für die spätere Beschriftung die Prozentzahl zu erhalten, multipliziere den Quotient mit 100: 0,1943 · 100 = 19 %. |
3400:17500=0,19429…≈0,1943 0,1943·100=19% |
|
6.
Damit du eine Gradzahl erhältst, multiplizierst du den prozentualen Wert mit 360: 0,1943 · 360 = 70°. |
0,1943·360=69,948°≈70° |
|
7.
Der erste Sektor (Teilfläche) des Kreisdiagramms hat eine Winkelweite von 70°. Lege das Geodreieck mit der langen Kante an die zuletzt gezeichnete senkrechte Linie. Verschiebe das Geodreieck soweit, bis die Nullmarkierung am Kreismittelpunkt liegt. |
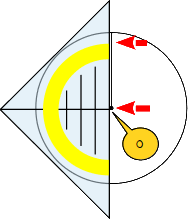 |
|
8.
Drehe das Geodreieck soweit nach unten, bis die 70°-Markierung der äußeren Skala durch die Linie geht. Achte beim Drehen darauf, dass sich die Nullmarkierung nicht verschiebt. |
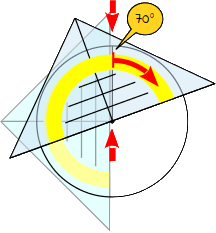 |
|
9.
Zeichne eine gerade Linie entlang dem Geodreieck vom Kreismittelpunkt bis zur Kreisaußenlinie. Lass das Geodreieck nach dem Zeichnen so liegen. Die von beiden Linien eingeschlossene Fläche entspricht dem ersten Wert (Januar). |
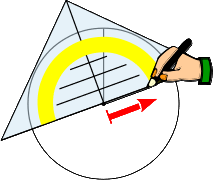 |
|
10.
Berechne für den zweiten Wert (Februar) die Winkelweite: Dividiere dazu den zweiten Wert (4.300) durch die Gesamtsumme und multipliziere den Quotient mit 360: 4.300 : 17.500 = 0,2457 · 360 = 88°. Multipliziere für die spätere Beschriftung den Quotient mit 100: 0,2457 · 100 = 25 %. |
4300:17500=0,24571…≈0,2457 0,2457·360=88,452°≈88° 0,2457·100=25% |
|
11.
Der zweite Sektor des Kreisdiagramms hat eine Winkelweite von 88°. Drehe das Geodreieck weiter nach oben, bis die 88°-Markierung der äußeren Skala durch die Linie geht. Achte wieder beim Drehen darauf, dass sich die Nullmarkierung nicht verschiebt. |
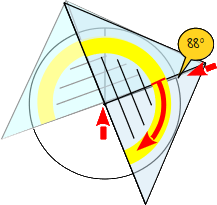 |
|
12.
Zeichne eine gerade Linie entlang dem Geodreieck vom Kreismittelpunkt bis zur Kreisaußenlinie. |
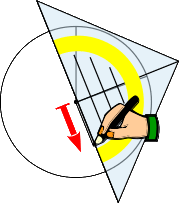 |
|
13.
Berechne für die weiteren Werte (März bis Mai) die Winkelweiten und zeichne sie in das Kreisdiagramm. |
 |
|
14.
Beschrifte das Kreisdiagramm: Schreibe neben dem Monatsnamen auch die von dir berechnete Prozentzahl dazu. Beginne mit dem Sektor oben rechts und beschrifte alle Sektoren im Uhrzeigersinn. |
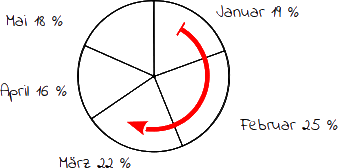 |
|
15.
Male zum Schluss die einzelnen Sektoren bunt aus. |
 |
Ein Kreisdiagramm wird verwendet, wenn Daten einer Tabelle grafisch in Form eines Kreises dargestellt werden sollen. Es lässt sich so leichter der Zusammenhang zwischen den Größen erkennen.
Das könnte dich auch interessieren
Du hast einen Fehler gefunden oder möchtest uns eine Rückmeldung zu diesem Eintrag geben? Rückmeldung geben