Kürzen
Brüche haben die Eigenschaft, dass du nur deren Aussehen (also die Zahlen) ändern kannst, ohne dass sich der eigentliche Wert des Bruches verändert. Beim so genannten Kürzen werden der Zähler und der Nenner eines Bruches mit der gleichen Zahl dividiert. Die beiden Zahlen des Bruches, also Zähler und Nenner, werden dabei kleiner. Es wird hierbei nur das Aussehen (die Zahlen) des Bruches geändert. Da du beide beide Zahlen mit der gleichen Zahl dividierst, verändern sie sich auch gleich. Das Verhältnis der Zahlen zueinander bleibt dabei gleich, damit verändert sich der eigentliche Wert des Bruches auch nicht.
Kürzen verändert nur das zahlenmäßige Aussehen des Bruches. Der eigentliche Wert des Bruches bleibt dabei erhalten.
Das Kürzen wird dazu verwendet, um Brüche gleichnamig zu machen. Dies ist bei der Addition und Subtraktion von Brüchen wichtig, da du nur gleichnamige Brüche, also Brüche mit dem gleichen Nenner, addieren bzw. subtrahieren kannst. Durch das Kürzen werden die unterschiedlichen Nenner auf ein gleiches, gemeinsames Vielfaches gebracht. Das Kürzen kannst du übrigens jederzeit anwenden. Durch das Kürzen werden die Zahlen im Bruch (sowohl im Zähler als auch im Nenner) kleiner. Und mit kleineren Zahlen rechnet es sich viel leichter. Bei vielen, meist einfachen Brüchen siehst du sofort, mit welcher Zahl du den Bruch kürzen musst. Leichter tust du dich auf jeden Fall, wenn du fit im Ein-mal Eins bist. Wenn du wie im nachfolgenden Beispiel sofort siehst, mit welcher Zahl du den Zähler und den Nenner jeweils dividieren musst, kannst du es natürlich gleich tun und den neuen gekürzten Bruch berechnen.
Du darfst das Kürzen von Brüchen nicht mit der Division verwechseln! Bei der Division ändert sich der Wert des neues Bruches, beim Kürzen ändert sich nur das Aussehen.
| So kürzt du einen Bruch: | So sieht's aus: |
|---|---|
| Dieser Bruch soll mit 3 gekürzt werden. | 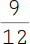 |
|
1.
Dazu dividierst du den Zähler und den Nenner jeweils mit der gleichen Zahl, nämlich der 3. |
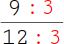 |
|
2.
Zuerst berechnest du den Zähler: 9 : 3 = 3. |
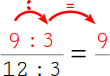 |
|
3.
Anschließend berechnest du den Nenner: 12 : 3 = 4. |
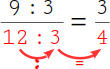 |
|
4.
Du erhältst nach dem Kürzen den Bruch |
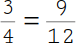 |
Beim Multiplizieren von Brüchen werden die Zähler der einzelnen Brüche miteinander multipliziert und die Nenner der einzelnen Brüche miteinander multipliziert.
Das könnte dich auch interessieren
Du hast einen Fehler gefunden oder möchtest uns eine Rückmeldung zu diesem Eintrag geben? Rückmeldung geben
 . Damit beschreibt
. Damit beschreibt 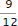 .
.