Brüche vereinfachen
Brüche haben die Eigenschaft, dass du nur deren Aussehen (also die Zahlen) ändern kannst, ohne dass sich der eigentliche Wert des Bruches verändert. Beim so genannten Kürzen werden der Zähler und der Nenner eines Bruches mit der gleichen Zahl dividiert. Die beiden Zahlen des Bruches, also Zähler und Nenner, werden dabei kleiner. Es wird hierbei nur das Aussehen (die Zahlen) des Bruches geändert. Da du beide Zahlen mit der gleichen Zahl dividierst, verändern sie sich auch gleich. Das Verhältnis der Zahlen zueinander bleibt dabei gleich, damit verändert sich der eigentliche Wert des Bruches auch nicht.
Kürzen verändert nur das zahlenmäßige Aussehen des Bruches. Der eigentliche Wert des Bruches bleibt dabei erhalten.
Durch das Kürzen werden die Zahlen im Bruch (sowohl im Zähler als auch im Nenner) kleiner. Und mit kleineren Zahlen rechnet es sich zudem viel leichter. Daher kannst du das Kürzen übrigens jederzeit anwenden. Bei vielen, meist einfachen Brüchen siehst du sofort, mit welcher Zahl du den Bruch kürzen musst, um ihn zu vereinfachen. Leichter tust du dich auf jeden Fall, wenn du fit im Einmaleins bist.
Du darfst das Kürzen von Brüchen nicht mit der Division verwechseln! Bei der Division ändert sich der Wert des neues Bruches, beim Kürzen ändert sich nur das Aussehen.
Du hast es jedoch nicht immer mit einfachen Brüchen zu tun, bei denen du auf den ersten Blick siehst, mit welcher Zahl du Zähler und Nenner kürzen kannst. Wenn du Brüche hast, bei denen die Zahlen dreistellig oder noch größer sind oder du auch bei kleineren Zahlen nicht darauf kommst, mit welcher Zahl zu kürzen ist, kannst du nach dem größten gemeinsamen Teiler (ggT) von Zähler und Nenner suchen. Da diese Zahl sowohl im Zähler wie auch im Nenner vorkommt, lässt sich der Bruch damit auf die kleinsten möglichen Zahlen kürzen.
Um diesen größten gemeinsamen Teiler zu finden, kannst du den »Euklidischen Algorithmus« anwenden. Dieser Algorithmus wurde nach dem griechischen Mathematiker Euklid (3. Jahrhundert v. Chr.) benannt, der ihn zu ersten Mal beschrieben hat. Dividiere dazu den Nenner ganzzahlig durch den Zähler. Geht die Division genau auf, kannst du mit dem Zähler den Bruch kürzen. In der Regel erhältst du dabei einen Rest. Subtrahiere nun diesen Rest vom Zähler. Nun vergleichst du den Rest der Division und die Differenz miteinander und dividierst den größeren Wert ganzzahlig durch den kleineren Wert.
Erhältst du dabei keinen Rest (Rest = 0), so ist der Rest von vorhin der größte gemeinsame Teiler. Mit dieser Zahl kannst du den Bruch kürzen. Erhältst du jedoch einen Rest, so haben der Zähler und der Nenner keinen größten gemeinsamen Teiler. Du kannst den Bruch nicht kürzen.
| So vereinfachst (kürzt) du einen Bruch: | So sieht es aus: |
|---|---|
| Dieser Bruch soll vereinfacht (gekürzt) werden. | 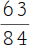 |
|
1.
Um den größten gemeinsamen Teiler (ggT) zu finden, dividiere zuerst den Nenner ganzzahlig durch den Zähler: 84 : 63 = 1 Rest 21. |
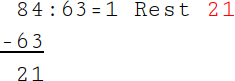 |
|
2.
Subtrahiere nun diesen Rest (die 21) vom Zähler: 63 – 21 = 42. |
63-21=42 |
|
3.
Nun vergleichst du den Rest (21) und die Differenz (42) miteinander und dividierst den größeren Wert ganzzahlig durch den kleineren Wert: 42 : 21 = 2 Rest 0. |
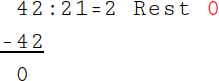 |
|
4.
Du erhältst keinen Rest (Rest = 0). Der Rest aus Schritt 1 ist der gesuchte größte gemeinsame Teiler (21). Mit dieser Zahl kannst du den Bruch kürzen. |
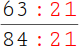 |
|
5.
Dividiere nun den Zähler durch den größten gemeinsamen Teiler (21): 63 : 21 = 3. |
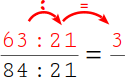 |
|
6.
Dividiere auch den Nenner durch den größten gemeinsamen Teiler: 84 : 21 = 4. |
 |
|
7.
Du erhältst nach dem Kürzen den Bruch |
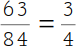 |
Solltest du im Schritt 3 (bei der zweiten Division) einen Rest erhalten, haben der Zähler und der Nenner keinen größten gemeinsamen Teiler. Du kannst den Bruch nicht weiter vereinfachen.
Um einen Bruch zu vereinfachen (kürzen) suchst du über den »Euklidischen Algorithmus« den größten gemeinsamen Teiler von Zähler und Nenner. Mit dieser Zahl kannst du anschießend den Bruch kürzen.
Das könnte dich auch interessieren
Du hast einen Fehler gefunden oder möchtest uns eine Rückmeldung zu diesem Eintrag geben? Rückmeldung geben
 . Damit beschreibt
. Damit beschreibt 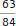 .
.