Multiplikation von Quadratwurzeln mit Koeffizienten
Das Wort Multiplikation stammt von dem lateinischen Wort »multiplicare« und bedeutet »vervielfachen«. Du vervielfachst also eine Zahl um eine andere. Dabei spielt es keine Rolle, ob du gewöhnliche (reelle) Zahlen multiplizierst oder ob es sich um eine Quadratwurzel (√b) handelt. Die Vorgehensweise ist wie bei der gewöhnlichen Multiplikation.
Eine Quadratwurzel ist ein mathematischer Ausdruck für  . Sie ist das Gegenteil des quadrierens, bei der du eine Zahl mit sich selber multiplizierst (x · x = x²). Eine Quadratwurzel besteht aus dem Wurzelzeichen (√) und einem Radikanden. So nennt man die Zahl unter der Wurzel. Nehmen wir mal als Beispiel √4. Der Radikand, also die Zahl unter der Wurzel ist 4.
. Sie ist das Gegenteil des quadrierens, bei der du eine Zahl mit sich selber multiplizierst (x · x = x²). Eine Quadratwurzel besteht aus dem Wurzelzeichen (√) und einem Radikanden. So nennt man die Zahl unter der Wurzel. Nehmen wir mal als Beispiel √4. Der Radikand, also die Zahl unter der Wurzel ist 4.
Versuche, bevor du mit deiner Multiplikation startest, ob du die Radikanden in eventuell vorhandene Quadratzahlen zerlegen kannst. Kannst du den Radikanden in eine Quadratzahl zerlegen, so ziehe aus ihr die Wurzel und schreibe das Ergebnis als Koeffizient vor die Wurzel. Der Rest verbleibt in der Wurzel. So stellst du sicher, dass du immer kleine Zahlen zum Rechnen hast.
Bei der Multiplikation von Quadratwurzeln geht du so vor, wie du es bei der Multiplikation von Zahlen gewöhnt bist: Du multiplizierst zuerst alle Radikanden miteinander, anschließend multiplizierst du alle Koeffizienten. Die Produkt aus zwei Quadratwurzeln ist wieder eine Quadratwurzel.
| So multiplizierst du Quadratwurzeln mit Koeffizienten: | So sieht's aus: |
|---|---|
| Du sollst diese Aufgabe lösen. | 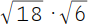 |
|
1.
Versuche die Radikanden in eventuell vorhandene Quadratzahlen zu zerlegen. Die 18 enthält eine Quadratzahl als 9 · 2. Du kannst daher diese Wurzel umschreiben in |
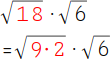 |
|
2.
Aus der 9 kannst du die Wurzel ziehen √9 = 3, da 3 · 3 = 9. Die 2 verbleibt in der Wurzel, die 3 schreibst du als Koeffizient vor die Wurzel. Du erhältst dann 3√2. |
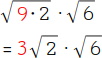 |
|
3.
Versuche auch den zweiten Radikanden in eventuell vorhandene Quadratzahlen zu zerlegen. Die Zahl 6 enthält jedoch keine Quadratzahlen, du kannst sie daher nicht weiter zerlegen. |
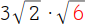 |
|
4.
Multipliziere anschließend die beiden Radikanden: 2 · 6 = 12. |
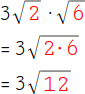 |
|
5.
Versuche den neuen Radikanden in eventuell vorhandene Quadratzahlen zu zerlegen. Die Zahl 12 besteht aus 4 · 3, denn die Zahl 4 ist eine Quadratzahl. Du kannst daher diese Wurzel umschreiben in |
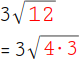 |
|
6.
Aus der 4 kannst du die Wurzel ziehen √4 = 2, da 2 · 2 = 4. Die 3 verbleibt in der Wurzel, die 2 schreibst du als Koeffizient vor die Wurzel. Du erhältst dann 2√3. |
 |
|
7.
Multipliziere zum Schluss die Koeffizienten: 3 · 2 = 6. |
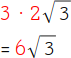 |
|
8.
Dein Ergebnis lautet 6√3. |
 |
Du kannst natürlich auch beide Wurzeln direkt miteinander multiplizieren. Multipliziere dazu einfach beide Radikanden miteinander: 18 · 6 = 108 (√18 · √6 = √108). Schön ist das Ergebnis jedoch nicht, da du es noch vereinfachen kannst. Du kannst den Radikand noch in die vorhandene Quadratzahlen zerlegen, was jedoch bei großen Zahlen wie 108 nicht mehr so einfach ist wie mit kleinen Zahlen. In √108 steckt √(36 · 3) und √36 = 6. Daher lautet dein Ergebnis wie oben auch 6.
Du multiplizierst zuerst alle Radikanden, anschließend alle Koeffizienten miteinander. Versuche dabei stets die Radikanten in eventuell vorhandene Quadratzahlen zu zerlegen.
Das könnte dich auch interessieren
Du hast einen Fehler gefunden oder möchtest uns eine Rückmeldung zu diesem Eintrag geben? Rückmeldung geben
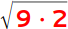 .
.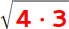 .
.