periodischer Dezimalbruch
Manche Divisionen haben ein Ergebnis, an dem du ewig rechnen würdest – es gibt kein Ende. Dies kann dir auch passieren, wenn du einen Bruch in eine Dezimalzahl umwandeln willst. Deine Dezimalzahl wird immer länger, aber es ist kein Ende in Sicht. Du kannst den Bruch nicht als Dezimalzahl schreiben. Viele solcher endlosen Rechnungen haben aber eine gewisse Regelmäßigkeit in ihrem Ergebnis. Wenn sich die Ziffern in regelmäßigen Abständen wiederholen, nennt man dies Periode oder man spricht von einer Periodizität.
Wenn du den Bruch 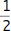 in eine Dezimalzahl umwandelst, erhältst du sehr schnell die kurze Dezimalzahl 0,5. Wenn du den Bruch
in eine Dezimalzahl umwandelst, erhältst du sehr schnell die kurze Dezimalzahl 0,5. Wenn du den Bruch  in eine Dezimalzahl umwandelst, musst du schon ein bisschen mehr rechnen und erhältst dann die schon etwas längere Dezimalzahl 0,0625. Wenn du dagegen den Bruch
in eine Dezimalzahl umwandelst, musst du schon ein bisschen mehr rechnen und erhältst dann die schon etwas längere Dezimalzahl 0,0625. Wenn du dagegen den Bruch  in eine Dezimalzahl umwandelst, hast du eine Aufgabe fürs Leben – du kannst ihn nicht als komplette Dezimalzahl schreiben. Die Dezimalzahl beginnt mit 0,3, gefolgt von unzähligen 3er, die sich immer wiederholen. Diese Wiederholung nennt man Periode.
in eine Dezimalzahl umwandelst, hast du eine Aufgabe fürs Leben – du kannst ihn nicht als komplette Dezimalzahl schreiben. Die Dezimalzahl beginnt mit 0,3, gefolgt von unzähligen 3er, die sich immer wiederholen. Diese Wiederholung nennt man Periode.
Wenn du eine solche Periode feststellst, dann brauchst du sie nur einmal hinschreiben und machst anschließend einen Strich über die sich wiederholenden Ziffern. Und schon bist du fertig. Allerdings darfst du die Stellen, die vor der Periode stehen, nicht weglassen. Du musst sie trotzdem hinschreiben.p
Da diese Brüche beim Umwandeln eine Periode aufweisen, nennt man solche Brüche auch periodische Dezimalbrüche.
| So entsteht ein periodischer Dezimalbruch: | So sieht's aus: |
|---|---|
| Du sollst die Brüche in eine Dezimalzahl umwandeln: |  |
|
1.
Dividiere beim ersten Bruch den Zähler durch den Nenner: 1 : 3. |
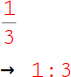 |
|
2.
Die Rechnung 1 : 3 ergibt ein nie abbrechendes Ergebnis: 0,3333333333333333333333…. |
 |
|
3.
Das Ergebnis besteht nur aus der Ziffer 3, die sich immer wieder wiederholt. Daher handelt es sich hier um eine Periode. Schreibe die 3 einmal hin und ziehe über sie einen Strich, damit kennzeichnest du die Periode. |
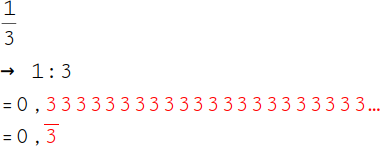 |
|
4.
Dividiere auch beim zweiten Bruch den Zähler durch den Nenner: 1 : 6. |
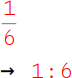 |
|
5.
Die Rechnung 1 : 6 ergibt ein nie abbrechendes Ergebnis: 0,1666666666666666666666…. |
 |
|
6.
Das Ergebnis besteht aus der Ziffer 1 gefolgt von der Ziffer 6, die sich immer wieder wiederholt. Daher handelt es sich hier um eine Periode. Schreibe die 6 einmal hinter die 1 und ziehe über sie einen Strich, damit kennzeichnest du die Periode. |
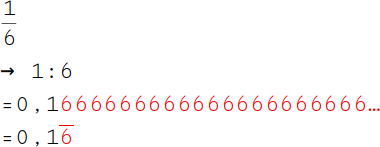 |
Wenn ein Bruch beim Umwandeln in eine Dezimalzahl eine Periode aufweist, nennt man diesen Bruch auch periodischer Dezimalbruch.
Das könnte dich auch interessieren
Du hast einen Fehler gefunden oder möchtest uns eine Rückmeldung zu diesem Eintrag geben? Rückmeldung geben