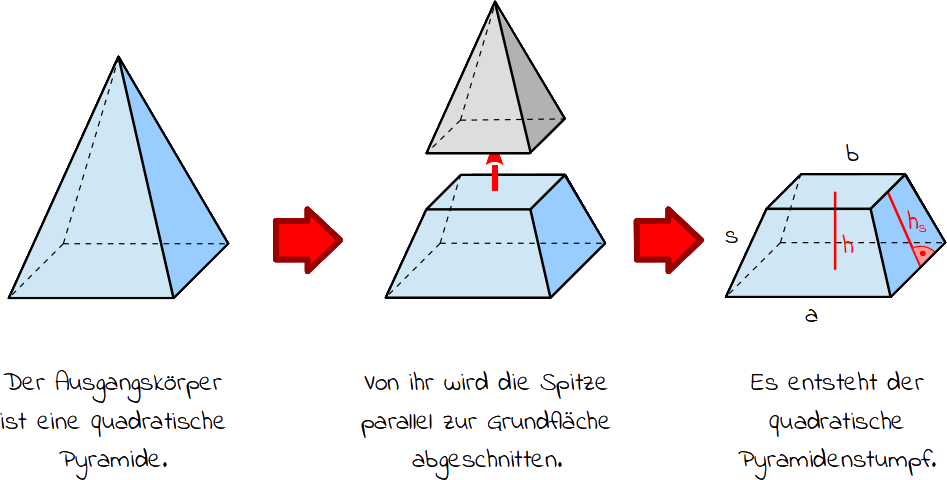
quadratischer Pyramidenstumpf

Ein quadratischer Pyramidenstumpf ist ein mathematischer Körper, der entsteht, wenn du von einer quadratischen Pyramide die Spitze parallel zur Grundfläche abschneidest. Seine Grund- und Deckfläche bildet ein Quadrat. Seine 4 Seitenflächen sind gleichschenklige Trapeze (Vierecke) und alle gleich groß. Er besteht also insgesamt aus 6 Flächen. Seine 12 Kanten bilden zusammen 8 Ecken.

Formeln

Volumen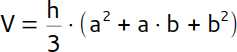
Oberfläche	O = G + M + D = a² + 2 · (a + b) · hs + b²
Mantel	M = 2 · (a + b) · hs
Grundfläche	G = a · a = a²
Deckfläche	D = b · b = b²
Seitenfläche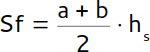
Seitenflächenhöhe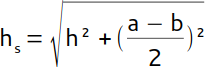

Der quadratische Pyramidenstumpf entsteht, wenn du von einer quadratischen Pyramide die Spitze parallel zur Grundfläche abschneidest. Er besitzt ein Quadrat als Grund- und Deckfläche. Er hat vier Seitenflächen, die gleich große gleichschenklige Trapeze darstellen.