Satz des Pythagoras

Der Satz des Pythagoras ist ein Satz in der Geometrie. Dieser Lehrsatz stammt vermutlich nicht von Pythagoras, sondern bereits aus dem mesopotamischen Kulturkreis um 2000 v. Chr. Über den Satz des Pythagoras kannst du Streckenlängen in einem rechtwinkligen Dreieck berechnen. Der Satz des Pythagoras lautet:

a² + b² = c²

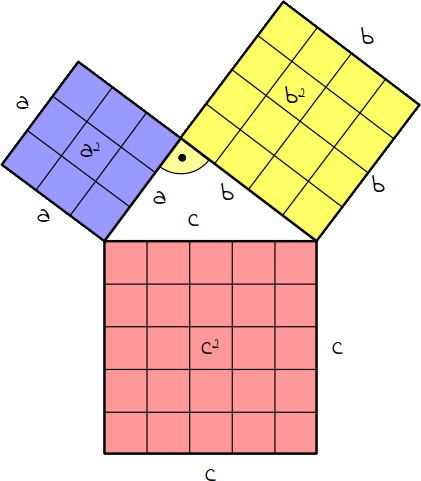
Du hast ein rechtwinkliges Dreieck mit den Seitenlängen a = 3 cm, b = 4 cm und c = 5 cm. Wenn du nun an Seite a ein Quadrat anfügt, dass die Seitenlänge a besitzt, so hat das Quadrat einen Flächeninhalt von 9 cm² (3 cm · 3 cm). Wenn du nun auch an Seite b ein Quadrat anfügt, dass die Seitenlänge b besitzt, so hat das Quadrat einen Flächeninhalt von 16 cm² (4 cm · 4 cm). Das Ganze machst du nun noch mit der Seite c. Das Quadrat mit der Seitenlänge c hat einen Flächeninhalt von 25 cm² (5 cm · 5 cm). Addierst du den Flächeninhalt der beiden kleineren Quadrate (9 cm² + 16 cm² = 25 cm²), so stellst du fest, dass die Summe den gleichen Flächeninhalt ergibt wie der Flächeninhalt des großen Quadrats (25 cm²).

Über diese Quadratbildung kannst du nun eine fehlende Seitenlänge des rechtwinkligen Dreiecks berechnen. Wenn dir die längste Seite fehlt, so quadrierst du beide kurzen Seiten, addierst sie und ziehst daraus die Wurzel, um die Länge zu erhalten: 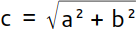. Die Wurzel benötigst du, um das Quadrat aufzulösen. Sie ist die Umkehroperation des Quadrierens. Wenn dir eine der kürzeren Seiten fehlt, beispielsweise Seite a, so quadrierst du die lange und die kurze Seite, subtrahierst die kurze Seite von der langen Seite und ziehst daraus die Wurzel, um die Länge zu erhalten: .

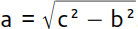So wendest du den Satz des Pythagoras an:	So sieht's aus:
In einem rechtwinkliges Dreieck sind alle Seite gegeben. Du sollst nun mit Hilfe des Satz des Pythagoras überprüfen, ob die Länge der Seite a und c stimmt.	a=3cm b=4cm c=5cm
1. Als erstes sollst du die Seite a überprüfen. Quadriere die Seite b und die Seite c: b² = (4 cm)² = 16 cm² und c² = (5 cm)² = 25 cm².	b²=(4cm)²=4cm·4cm=16cm² c²=(5cm)²=5cm·5cm=25cm²
2. Subtrahiere nun das Quadrat der kurzen Seite (b²) von dem Quadrat der langen Seite (c²): c² – b² = 25 cm² – 16 cm² = 9 cm².	c²-b² =25cm²-16cm² =9cm²
3. Ziehe aus dem Ergebnis die Wurzel, um die Länge der Seite a zu erhalten: a = √9cm² = 3 cm.	a=√9cm² a=3cm
4. Die Länge der Seite a = 3 cm stimmt.	a=3cm
5. Als zweites sollst du die Seite c überprüfen. Quadriere die Seite a und die Seite b: a² = (3 cm)² = 9 cm² und b² = (4 cm)² = 16 cm².	a²=(3cm)²=3cm·3cm=9cm² b²=(4cm)²=4cm·4cm=16cm²
6. Addiere nun das Quadrat der kurzen Seiten (a² und b²): a² + b² = 9 cm² + 16 cm² = 25 cm².	a²+b² =9cm²+16cm² =25cm²
7. Ziehe aus dem Ergebnis die Wurzel, um die Länge der Seite c zu erhalten: c = √25cm² = 5 cm.	c=√25cm² c=5cm
8. Die Länge der Seite c = 5 cm stimmt.	c=5cm