Berechnung beliebiger Dreiecke

Den Umfang oder den Flächeninhalt eines Dreiecks zu berechnen ist nicht sonderlich schwer: Beim Umfang zählst du einfach alle drei Seiten zusammen. Beim Flächeninhalt multiplizierst du die Länge mit der Höhe und teilst anschließend alles durch zwei. Was sich jedoch so leicht anhört wird oft zu einem unüberwindbarem Hindernis: Denn meistens fehlt dir eine benötigte Seite oder du kannst mit den gegebenen Seiten nichts anfangen.

Aber es gibt Abhilfe, denn es gibt nichts, was Mathematiker nicht können! Denn unter Zuhilfenahme der drei Winkelfunktionen Sinus, Cosinus und Tangens kannst du dir die fehlende Stücke eines beliebigen Dreiecks aus den anderen gegebenen Stücken berechnen. Auch über den Satz des Pythagoras kannst du dir Stecken errechnen. Der einzige Haken an der Sache ist, du benötigst für die Winkelfunktionen sowie für den Satz des Pythagoras jeweils ein rechtwinkliges Dreieck. Das heißt, wenn du kein rechtwinkliges Dreieck hast, teilst du das Dreieck einfach in geschickte Teildreiecke, die einen rechten Winkel besitzen. Dies erreichst du, indem du Höhen einzeichnest. Da Höhen immer im rechten Winkel zu einer Seite stehen, bekommst du automatisch den rechten Winkel. Wichtig ist aber, dass du die Höhen immer so einzeichnest, dass du keine gegebenen Maße teilst. Anschließend kannst du dir die fehlenden Stücke aus den anderen gegebenen Stücken berechnen.

So berechnest du beliebige Dreiecke:	So sieht's aus:
Du sollst den Umfang u (u = a + b+ c) des folgenden Dreiecks berechnen.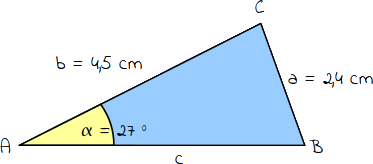
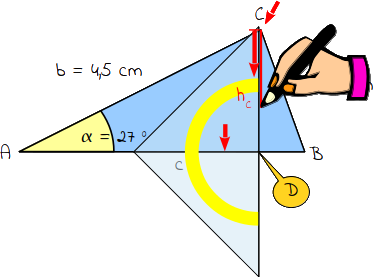
1. Um den Umfang zu berechnen benötigst du die Länge von allen 3 Seiten. Du hast jedoch nur 2 Seiten gegeben (Seite a und b). Du musst daher das DreieckACD in zwei rechtwinklige Dreiecke teilen. Zeichne dazu eine geeignete Höhe ein. Da du die Länge der Seite b und der Seite a gegeben hast, zeichnest du die Höhe hc ein, da du hier keine gegebenen Maße teilst. Dort, wo die Höhe hc auf der Seite c endet, befindet sich der Punkt D.
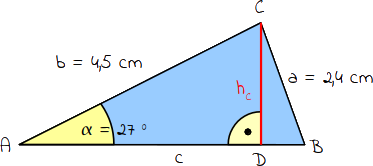
2. Du erhältst zwei rechtwinklige Dreiecke (das DreieckACD und das DreieckBCD).
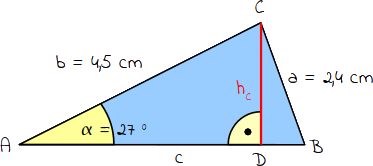
3. Nun kannst du über den Sinus die Länge der Höhe hc ausrechnen. Die Seite hc ist die Gegenkathete zum Winkel α. Die Seite b ist die längste Seite im DreieckACD und die Hypotenuse. Du erhältst als Seite hc = 2,0 cm.
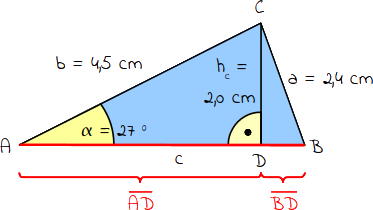
4. Jetzt hast du die Länge der Höhe hc berechnet. Um den Umfang zu berechnen, benötigst du noch die Länge der Seite c. Dazu musst du die Seite c in die Strecke AD und Strecke BD zerlegen.
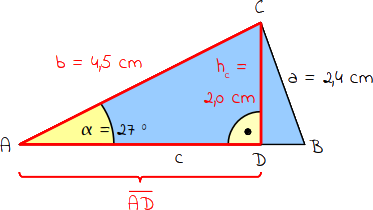
5. Berechne nun die Länge der Strecke AD. Verwende hierzu den Satz des Pythagoras: a² + b² = c². Da du dich im DreieckACD befindest, ist a = hc, b = AD und c = b. Dementsprechend lautet deine Formel: hc² + AD² = b². Die Länge der Strecke AD beträgt 4,0 cm.
6. Auf die gleiche Art berechnest du nun die Länge der Strecke BD. Verwende auch hierzu den Satz des Pythagoras. Da du dich jetzt im DreieckBCD befindest, ist a = BD, b = hc und c = a. Dementsprechend lautet deine Formel: BD² + hc² = a². Die Länge der Strecke BD beträgt 1,3 cm.
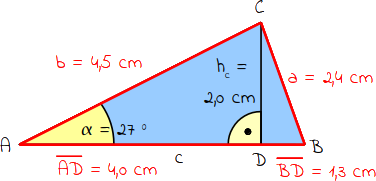
7. Jetzt kannst du den Umfang u berechnen. Addiere dazu alle 4 Seiten zusammen: a + b + AD + BD = 12,2 cm.
8. Der Umfang u des DreiecksABC beträgt 12,2 cm.	u=12,2cm

Über die Winkelfunktionen und den Satz des Pythagoras kannst du dir in einem Dreieck fehlende Stücke berechnen. Du brauchst dazu jedoch ein rechtwinkliges Dreieck. Wenn du keins vorliegen hast, musst dein Dreieck durch Höhen in rechtwinklige Teildreiecke aufteilen.