Scheinbruch
Eigentlich haben alle Brüche eins gemeinsam: Der Zähler ist vom Wert her immer kleiner als der Nenner. Dieser Bruch stellt somit einen Wert bzw. eine Zahl dar, die kleiner als 1 ist. Wenn nun die Zahl im Zähler genau so groß ist wie die Zahl im Nenner, handelt es sich um einen Scheinbruch, z. B. 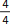 . Dieser Bruch stellt somit einen Wert bzw. eine Zahl dar, der genau 1 ist. Du teilst ein Ganzes in 4 Stücke und nimmst davon 4 Stücke, so hast du wieder das Ganze. Es handelt sich daher bei
. Dieser Bruch stellt somit einen Wert bzw. eine Zahl dar, der genau 1 ist. Du teilst ein Ganzes in 4 Stücke und nimmst davon 4 Stücke, so hast du wieder das Ganze. Es handelt sich daher bei 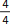 eigentlich um eine Ganzzahl (nämlich 1) und ist somit gar kein Bruch. Daher nennt man solche Brüche auch Scheinbrüche. Es handelt sich auch dann um einen Scheinbruch, wenn der Zählerwert das Doppelte, Dreifache, Vierfache usw. des Nennerwertes beträgt. Der Bruch
eigentlich um eine Ganzzahl (nämlich 1) und ist somit gar kein Bruch. Daher nennt man solche Brüche auch Scheinbrüche. Es handelt sich auch dann um einen Scheinbruch, wenn der Zählerwert das Doppelte, Dreifache, Vierfache usw. des Nennerwertes beträgt. Der Bruch  ist also auch ein Scheinbruch, da er die Ganzzahl 3 darstellt.
ist also auch ein Scheinbruch, da er die Ganzzahl 3 darstellt.
Wenn du einen Scheinbruch enttarnen willst, teile einfach den Zählerwert durch den Nennerwert. Das Ergebnis ist dann die Ganzzahl. Sollte sich der Zählerwert jedoch nicht ganzzahlig durch den Nennerwert teilen lassen, handelt es sich nicht um einen Scheinbruch, sondern um einen unechten Bruch.
| So wandelst du einen Scheinbruch in eine Ganzzahl um: | So sieht's aus: |
|---|---|
| Dieser Scheinbruch soll in eine Ganzzahl umgewandelt werden. |  |
|
1.
Um einen Scheinbruch zu enttarnen, teile einfach den Zähler (8) durch den Nenner (4). |
 |
|
2.
Berechne die Division: 8 : 4 = 2. |
8:4 =2 |
|
3.
Der Scheinbruch |
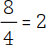 |
Theoretisch könntest du jede Ganzzahl als Bruch schreiben. Im Zähler würde der Wert der Ganzzahl stehen und der Nenner hätte den Wert 1, z. B.  . Da dieser Bruch kein Teil eines Ganzen darstellt, handelt es sich auch um einen Scheinbruch.
. Da dieser Bruch kein Teil eines Ganzen darstellt, handelt es sich auch um einen Scheinbruch.
Bei Scheinbrüchen ist der Zähler ein ganzzahliges Vielfaches des Nenners, also eine Ganzzahl und daher eigentlich kein „echter“ Bruch.
Das könnte dich auch interessieren
Du hast einen Fehler gefunden oder möchtest uns eine Rückmeldung zu diesem Eintrag geben? Rückmeldung geben
 stellt also 2 Ganze dar.
stellt also 2 Ganze dar.