umgekehrt proportionaler Dreisatz

Mit dem Dreisatz kannst du aus drei vorgegebenen Werten (a, b und c) über deren Verhältnis einen gesuchten vierten Wert (x) berechnen. Das hört sich zwar zunächst recht kompliziert an, ist es aber nicht. Denn du kannst mit dem Dreisatz Aufgaben sehr einfach und anschaulich lösen, ohne große mathematische Kenntnisse anwenden zu müssen. Du brauchst dazu nur die Multiplikation und die Division, mehr nicht. Der Dreisatz macht sich dabei das Verhältnis zunutze, das zwischen den Zahlen herrscht:

a zu b verhält sich wie c zu x

Der Dreisatz ähnelt in der Anwendung dem Zweisatz. Er besteht im Grunde aus zwei Zweisätzen, die nacheinander berechnet werden. Im Gegensatz zum Zweisatz ist der Wert a und der Wert c nicht durch die gleich Zahl teilbar.

Der Ausgangspunkt beim Dreisatz ist das Verhältnis zwischen zwei Zahlen bzw. Größen: a zu b – der erste Zweisatz. Dieses Verhältnis ist bereits vorgegeben und bleibt immer erhalten. Beim Dreisatz ist der erste Zweisatz jedoch fest vorgegeben: Du rechnest immer auf den Wert 1. Dies erreichst du, indem du durch den Wert a dividierst.

Beim ersten Zweisatz gilt der Erkennungssatz »je weniger, desto mehr«. Das bedeutet, wenn du auf der linken Seite den Wert a verringerst, also dividierst, vermehrt sich der Wert b um das gleiche Verhältnis. Daher musst du nun den Wert b mit a multiplizieren. Jetzt hast du die Einheit (1) ausgerechnet. Von diesem Wert 1 rechnest du auf den Wert c, in dem du die 1 mit c multiplizierst - der zweite Zweisatz. Beim diesem Zweisatz gilt der Erkennungssatz »je mehr, desto weniger«. Aufgrund des Verhältnisses, dass zwischen c und x besteht, musst du jetzt den neuen Wert b mit c dividieren. Da du beide Werte jeweils mit der umgekehrten Rechenart berechnest, nennt man diese Art von Dreisatz auch umgekehrt proportionaler Dreisatz, weil sich alle Größen proportional (im gleichen Verhältnis), aber andersherum verändern.

Nehmen wir an, 3 Maler brauchen 6 Tage, um ein Haus zu streichen. Du sollst nun berechnen, wie lange 4 Maler dafür brauchen.

Das Verhältnis in dieser Aufgabe lautet: 3 zu 6 verhält sich wie 4 zu x. Um den gesuchten Wert x (die neue Zeit) zu erhalten, musst du zuerst auf die Einheit (1 Maler) herunter rechnen. Um von 3 auf 1 Maler zu kommen, musst du durch 3 dividieren. Das erste Verhältnis lautet daher „geteilt durch 3“ (: 3). Bei diesem Zweisatz gilt der Erkennungssatz »je weniger, desto mehr«. Das bedeutet, 1 Maler braucht logischerweise länger als 3 Maler. Daher drehst du dieses Verhältnis um und wendest es auf den Wert b (6 Tage) an: aus „geteilt durch 3“ wird „mal 3“ (6 Tage · 3 = 18 Tage) Damit hast du nun die Dauer für 1 Maler berechnet.

Um von 1 auf 4 Maler zu kommen, musst du mit 4 multiplizieren. Das zweite Verhältnis lautet daher „mal 4“ (· 4). Beim diesem Zweisatz gilt der Erkennungssatz »je mehr, desto weniger«. Das bedeutet, 4 Maler brauchen logischerweise weniger Zeit als 1 Maler. Dieses Verhältnis drehst du um und wendest es auf die 18 Tage an: aus „mal 4“ wird „geteilt durch 4“ (18 Tage : 4 = 4,5 Tage) Damit hast du nun die Dauer für 4 Maler berechnet (zweiter Zweisatz).

So wendest du den Dreisatz an:	So sieht's aus:
Du sollst diese Aufgabe lösen.	3 Maler → 6 Tage 1 Maler → x
1. Bestimme zunächst das erste Verhältnis: Um von 3 Maler auf 1 Maler zu kommen, musst du durch 3 dividieren (3 : 3 = 1). Dein Verhältnis lautet „geteilt durch 3“.
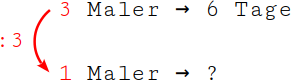2. Dividiere nun den linken Wert mit dem Verhältnis „geteilt durch 3“: 3 Maler : 3 = 1 Maler.
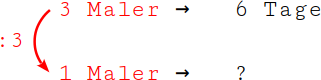3. Dieses Verhältnis drehst du um und wendest es auf den rechten Wert an: aus „geteilt durch 3“ wird „mal 3“. Multipliziere ihn mit 3: 6 Tage · 3 = 18 Tage. Damit hast du nun die Dauer von einer Einheit (also 1 Maler) berechnet.
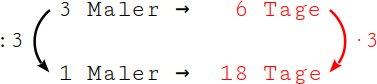4. Bestimme dann das zweite Verhältnis: Um von 1 Maler auf 4 Maler zu kommen, musst du mit 4 multiplizieren (1 · 4 = 4). Dein Verhältnis lautet „mal 4“.
5. Multipliziere nun den linken Wert mit dem Verhältnis „mal 4“: 1 Maler · 4 = 4 Maler.
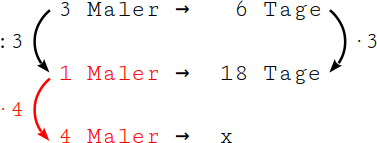6. Dieses Verhältnis drehst du wieder um und wendest es auf den rechten Wert an: aus „mal 4“ wird „geteilt durch 4“. Dividiere ihn durch 4: 18 Tage : 4 = 4,5 Tage.

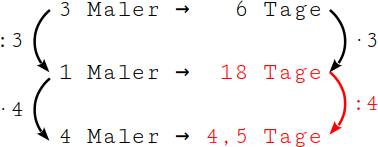Bei einem umgekehrt proportionalen Dreisatz verändern sich beide Seiten entgegengesetzt (umgekehrt), d.h. ver-mehrt sich die eine Seite, so vermindert sich die andere Seite um das umgekehrte Verhältnis. Daher spricht man auch vom Dreisatz mit ungeradem Verhältnis.