Punkte einer Parabel rechnerisch überprüfen
Du sollst zwei gegebene Punkte rechnerisch überprüfen, ob sie auf einer Parabel liegen, ohne sie dabei vorher zu zeichnen. Ein solcher Punkt besteht aus einer x- und einer y-Koordinate, wobei die y-Koordinate von der x-Koordinate abhängt. Das bedeutet, anhand der x-Koordinate kannst du die y-Koordinate bestimmen.
Die beiden Punkte sind P1 (-2|3) und P2 (4|6), die Gleichung der Parabel lautet y = x² - 1.
Die y-Werte bzw. die y-Koordinaten sind vom x-Wert abhängig. Setze dazu den x-Wert des ersten Punktes P1 (-2) in die Parabelgleichung ein. Sie lautet nun y = (-3)² - 1. Wenn du das ausrechnest, erhältst du einen y-Wert von 3. Dieser errechnete Wert entspricht auch der gegebenen y-Koordinate. Daher liegt dieser Punkt auf der Parabel.
Setze den x-Wert des zweiten Punktes P2 (4) ebenfalls in die Parabelgleichung ein. Sie lautet nun y = (4)² - 1. Wenn du das ausrechnest, erhältst du einen y-Wert von 15. Dieser errechnete Wert entspricht nicht der gegebenen y-Koordinate, da diese den Wert 6 hat. Daher liegt dieser Punkt nicht auf der Parabel.
| So überprüfst du Punkte einer Parabel: | So sieht's aus: |
|---|---|
| Die Gleichung der Parabel lautet: | y=x²-1 |
|
1.
Der erste Punkt P1 hat die Koordinaten (-2|3). Der x1-Wert beträgt -2 und der y1-Wert beträgt 3. |
x1=-2 x2=3 |
|
2.
Setze den x-Wert des ersten Punktes (x1) in die Gleichung ein. Das x1 in der Gleichung wird durch die -2 ersetzt. |
y1=(x1)¹-1 → x1=-2 y1=(-2)²-1 |
|
3.
Rechne nun die Gleichung aus, um den y1-Wert zu erhalten. Der erste y-Wert beträgt 3. |
y1=(-2)²-1 y1=4-1 y1=3 |
|
4.
Dieser errechnete Wert entspricht auch der gegebenen y‑Koordinate. Daher liegt dieser Punkt auf der Parabel. |
gegeben: y1=3 errechnet: y1=3 |
|
5.
Setze den x-Wert des zweiten Punktes (x2) in die Gleichung ein. Das x2 in der Gleichung wird durch die 4 ersetzt. |
y2=(x2)²-1 → x2=4 y2=(4)²-1 |
|
6.
Rechne nun die Gleichung aus, um den y2-Wert zu erhalten. Der zweite y-Wert beträgt 15. |
y2=(4)²-1 y2=16-1 y2=15 |
|
7.
Dieser errechnete Wert entspricht nicht der gegebenen y‑Koordinate. Daher liegt dieser Punkt nicht auf der Parabel. |
gegeben: y2=6 errechnet: y2=15 |
Zeichnest du die beiden Punkte und die Parabel mit der Gleichung y = x² - 1 in ein Koordinatensystem, so siehst du, dass nur der Punkt P1 auf ihr liegt. Der Punkt P2 liegt nicht auf dieser Parabel, das du auch rechnerisch bewiesen hast.
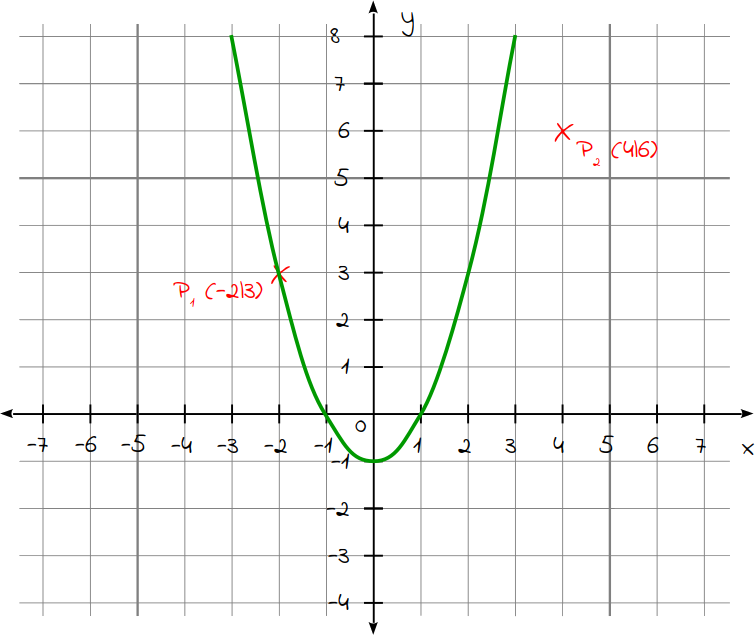
Um zu überprüfen, ob ein Punkt auf einer Parabel liegt, setzt du dessen x-Koordinate in die Gleichung der Parabel ein. Stimmt dieser errechnete y-Wert mit der gegebenen y‑Koordinate überein, liegt dieser Punkt auf der Parabel.
Das könnte dich auch interessieren
Du hast einen Fehler gefunden oder möchtest uns eine Rückmeldung zu diesem Eintrag geben? Rückmeldung geben