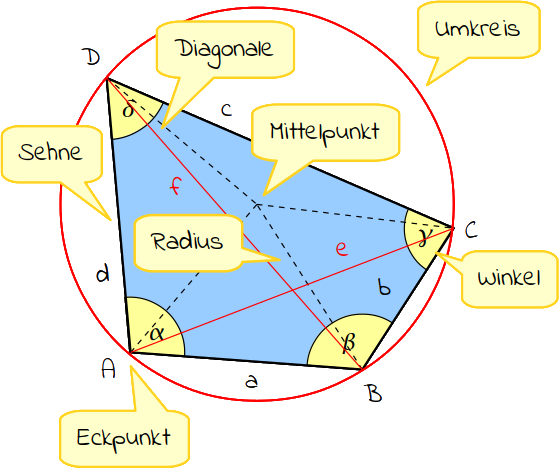
Sehnenviereck

Ein Sehnenviereck ist ein spezielles Viereck, denn seine vier Seiten sind alles Sehnen. Eine Sehne ist eine Strecke, die einen Punkt auf der Kreisaußenlinie mit einen weiteren Punkt auf der Kreisaußenlinie verbindet. Diese Strecke geht dabei nicht durch den Mittelpunkt des Kreises. Da der Kreis durch alle Eckpunkte des Sehnenvierecks geht, wird er auch Umkreis genannt. Das Sehnenviereck hat eine besondere Eigenschaft: Die Summe der Produkte gegenüberliegender Seiten ist gleich dem Produkt der Diagonalen: (a · c) + (b · d) = e · f. Wenn du gegenüberliegende Winkel zusammenzählst (addierst), so sind deren Summen gleich groß (α + γ = β + δ).

Formeln

Flächeninhalt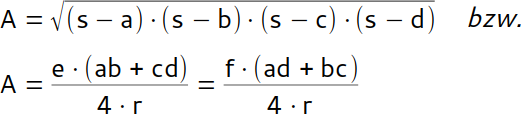
Umfang	u = a + b + c + d
Winkelsumme	α+ β + γ + δ = 360°

Ein Sehnenviereck ist eine Fläche, deren Seiten Sehnen eines Kreises sind. Alle Eckpunkte liegen auf einer gemeinsamen Kreisbahn, dem Umkreis.