Tangens

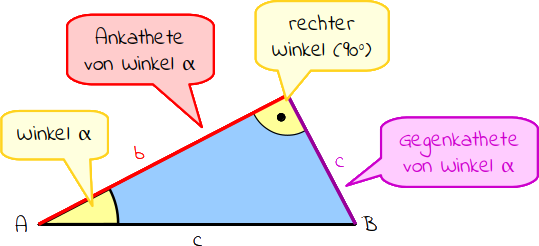
Ein Dreieck besteht bekanntlich aus drei Ecken mit drei Winkeln. Zwischen diesen drei Ecken befinden sich drei Seiten. Zu den besonderen Dreiecken gehört das rechtwinklige Dreieck, bei dem einer der Winkel rechtwinklig ist. Sind die Längen von einzelnen Seiten im rechtwinkligen Dreieck bekannt, lassen sich die Maße der Winkeln berechnen. Dazu benötigst du die sogenannten Winkelfunktionen.

Der Tangens ist eine dieser Winkelfunktion und wird mit tan abgekürzt. Mit ihm kannst du den Winkel berechnen, der an einer der beiden bekannten Seiten anliegt. Der Tangens ist nämlich das Verhältnis der Länge der Gegenkathete (das ist die Seite, die dem Winkel gegenüberliegt) zur Länge der Ankathete (das ist die Seite, die an dem Winkel anliegt).

Die Bezeichnung Tangens stammt von dem Mathematiker Thomas Finck (1561–1656), der sie 1583 einführte.

So berechnest du über den Tangens den Winkel α:	So sieht's aus:
Du sollst den Winkel α berechnen. In deinem rechtwinkligen Dreieck ist gegeben: Gegenkathete mit 3 cm und Ankathete mit 4 cm.	Gegenkathete 3cm Ankathete 4cm α=?
Das ist deine Formel für den Winkel α.
1. Setzte nun die gegebenen Werte in diese Formel ein: Die Länge für die Gegenkathete beträgt 3 cm.
2. Die Länge für die Ankathete beträgt 4 cm.
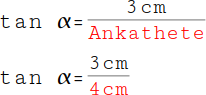3. Nun benötigst du einen Taschenrechner, um den Wert für den Winkel α auszurechnen. Tippe dazu folgendes ein:
4. Als Wert für den Winkel α erhältst du 37°.