Division von komplexen Zahlen
Das Wort Division stammt von dem lateinischen Wort »divisio« und bedeutet »teilen«. Du teilst also eine Zahl durch eine andere Zahl. Dabei spielt es keine Rolle, ob du gewöhnliche (reelle) Zahlen oder komplexe Zahlen teilst. Die Vorgehensweise ist wie bei der gewöhnlichen Division.
Eine komplexe Zahl ist eine imaginäre Zahl. Das bedeutet, es ist eine Zahl, die du nicht aufschreiben kannst, wie z. B. 16 oder 21. Es handelt sich bei einer komplexen Zahl um eine unvorstellbare Zahl. Sie existiert nur in unserer Phantasie zur besseren Vorstellung. Damit du sie jedoch aufschreiben kannst, wird für diese Zahlen der Buchstabe i (von imaginär) verwendet.
Die Division von komplexen Zahlen schreibst du am besten als Bruch. Der Dividend bildet den Zähler und der Divisor den Nenner. Erweitere zuerst den Bruch mit dem Nenner. Drehe dabei jedoch das Vorzeichen der komplexen Zahl um. Aus +16i wird dann ein -16i. Multipliziere anschließend die ganzen Klammern im Zähler und im Nenner aus, wobei sich im Nenner die 3. binomische Formel befindet. Die komplexe Zahl im Nenner verschwindet, da das i zu einem i² wird, das durch ein -1 ersetzt wird. Fasse anschließend die Zahlen im Zähler und Nenner zusammen. Der Quotient aus zwei komplexen Zahlen ist wieder eine komplexe Zahl bzw. ein komplexer Bruch.
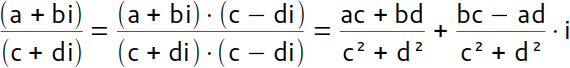
| So dividierst du komplexe Zahlen: | So sieht's aus: |
|---|---|
| Du sollst diese Aufgabe lösen. | 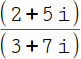 |
|
1.
Erweitere den Bruch mit dem Nenner. Allerdings musst du das Vorzeichen der komplexen Zahl (7i) umdrehen. Aus +7i wird -7i. Du erweiterst also mit (3 - 7i). |
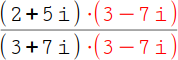 |
|
2.
Nun multiplizierst du die ganzen Klammern aus. Wir beginnen im Zähler und multiplizieren die erste Zahlen in der ersten Klammern mit beiden Zahlen der zweiten Klammer: 2 · 3 = 6 und 2 · -7i = -14i. |
 |
|
3.
Multipliziere auch die zweite Zahl in der ersten Klammer mit beiden Zahl in der zweiten Klammer: 5i · 3 = 15i und 5i · -7i = -35i². |
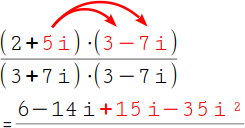 |
|
4.
Du hast nun eine komplexe Zahl mit einem i². Dieses i² wird durch ein -1 ersetzt. Da zwischen der Zahl und dem i² ein Malpunkt steht, lautet deine neue letzte Zahl nun –35 (·) -1 = +35. |
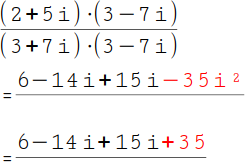 |
|
5.
Nun multiplizierst du die ganzen Klammern im Nenner aus. Es handelt sich hierbei um die 3. binomische Formel: (3 + 7i) · (3 – 7i) = 9 - 49i². |
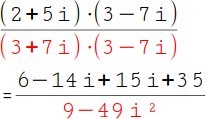  |
|
6.
Du hast nun wieder eine komplexe Zahl mit einem i². Auch dieses i² wird durch ein -1 ersetzt. Deine neue letzte Zahl lautet nun –49 (·) -1 = +49. |
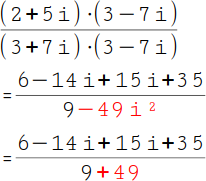 |
|
7.
Bringen wir zunächst etwas Ordnung in den Bruch: Im ersten Schritt vertauschen wir die -14i mit der +35. Damit stehen nun die gleichen Zahlen zusammen. |
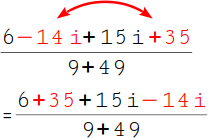  |
|
8.
Im zweiten Schritt fassen wir zusammen. Zuerst die ersten beiden Zahlen im Zähler: 6 + 35 = 41. |
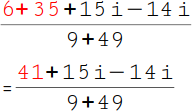 |
|
9.
Anschließend fassen wir noch die letzten beiden Zahlen im Zähler zusammen: 15i - 14i = i. |
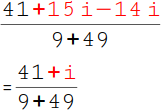 |
|
10.
Dein Bruch ist schon ziemlich geschrumpft. Rechne nun zum Schluss noch deinen Nenner aus und du bist fertig: 9 + 49 = 58. |
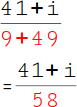 |
|
11.
Dein Ergebnis lautet |
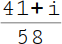 |
Das könnte dich auch interessieren
Du hast einen Fehler gefunden oder möchtest uns eine Rückmeldung zu diesem Eintrag geben? Rückmeldung geben
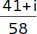 .
.