Division von Quadratwurzeln

Das Wort Division stammt von dem lateinischen Wort »divisio« und bedeutet »teilen«. Du teilst also eine Zahl durch eine andere Zahl. Dabei spielt es keine Rolle, ob du gewöhnliche (reelle) Zahlen oder ob es sich um eine Quadratwurzel (√b) handelt. Die Vorgehensweise ist wie bei der gewöhnlichen Division.

Eine Quadratwurzel ist ein mathematischer Ausdruck für x^½. Sie ist das Gegenteil des quadrierens, bei der du eine Zahl mit sich selbst multiplizierst (x · x = x²). Eine Quadratwurzel besteht aus dem Wurzelzeichen (√) und einem Radikanden. So nennt man die Zahl unter der Wurzel. Nehmen wir mal als Beispiel √4. Der Radikand, also die Zahl unter der Wurzel ist 4.

Die Division von Quadratwurzeln schreibst du am Besten als Bruch: Der Dividend (die erste Wurzel) wird zum Zähler (obere Zahl des Bruches) und der Divisor (zweite Zahl) wird zum Nenner (untere Zahl des Bruches). Nun hast du einen Bruch, in dem zweimal eine Wurzel vorkommt. Dies kannst du auch anders schreiben: Du kannst auch eine große Wurzel über deinen Bruch schreiben. Unter der Wurzel steht dann ein Bruch aus den Radikanden (Zahl unter der Wurzel). Dividiere nun den Zähler (obere Zahl) durch den Nenner (untere Zahl). Da du eigentlich die Wurzel aus dem Bruch ziehen sollst, ziehst du eben jetzt die Wurzel aus dem Ergebnis. Schreibe dazu das Wurzelzeichen über dein Ergebnis. Der Quotient aus zwei Quadratwurzeln ist wieder eine Quadratwurzel.

	So sieht's aus:
Du sollst diese Aufgabe lösen.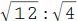
1. Schreibe diese Division als Bruch: Der Dividend (√12) wird zum Zähler (obere Zahl) und der Divisor (√4) wird zum Nenner (untere Zahl).
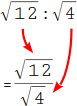2. Du kannst auch eine große Wurzel über deinen Bruch schreiben. Unter der Wurzel steht dann ein Bruch aus den Radianten (Zahl unter der Wurzel).
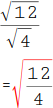3. Dividiere nun den Zähler (obere Zahl) durch den Nenner (untere Zahl): 12 : 4 = 3.
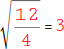4. Da du eigentlich die Wurzel aus dem Bruch ziehen sollst, ziehst du jetzt die Wurzel aus dem Ergebnis. Schreibe das Wurzelzeichen (√) über dein Ergebnis: aus 3 wird √3.
5. Dein Ergebnis lautet √3.